Verbogeometry -- Installment VII --- Pythagorean Theorem and The Distance Formula

2.6. The Distance Formula and Pythagorean Theorem: The distance formula uses the Pythagorean Theorem to calculate distances on the Cartesian coordinate system. The Pythagorean Theorem says that the hypotenuse of a right triangle is equal to the square of it sides. (see figure 26)


Figure. 26

solve for c and we get the following see figure 27


Figure. 27


Let us plot two points on a two-dimensional axis system P1(-9,10) and P2(4,3) and If we draw a lines between the points and lines parallel to the axes we can obtain a right triangle. (see figure 28)


Figure. 28

To solve the length of the hypotenuse we first find the difference between the x values and the y values to create the sides of the triangle then we plug the values into the Pythagorean Theorem.
x value is 9 - 4 = 5 and the y value is 10 - 3 = 7
Now we plug it to the equation and we get the expression in figure 29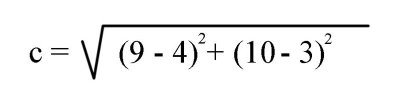


Figure 29

The distance or length of the hypotenuse would be the square root of 74 or approximately 8.602
The distance formula is thus:
Given two points (x1,y1) and (x2,y2) (see figure 30)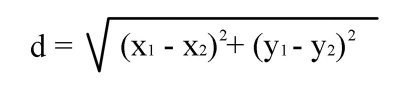


Figure 30

Now what we have been looking at up till now has been in two-dimensions but we can also express a distance in many dimensions. Let us look at two points in three dimensions.
P1(x1,y1,z1) P2(x2,y2,z2)
If we were to put these two points into the distance formula it would look like what is shown in figure 31


Figure 31

It is evident that we can use the distance formula in uncountable dimensions all we have to is to add another dimensional term to the formula for every dimension we wish to express.