The Virtuous Sphere (part one)

The Virtuous Sphere (part one)

I thought it would be a nice idea to post "The Virtuous Sphere" and talk some about it. First of all I would like to say that I believe there are many ways to define virtue, this is only an artist rendition of one way. Please do not get bound up here in the idea of some absolute truth… remember the Hindu saying: “All wars are Just on both sides” When this piece was originally mediated to me my intentions were not so much interested in an answer of denotation but in the aesthetic inherit with the structure of a mathematical sphere and the coloration and distortion of that sphere by the personal ideas of integrity, justice, nobility and of course virtue.

Today's blog entry will talk about the analytic geometry involved in the piece and the next blog entry will discuss the verbogeometrical ideas needed to approach this piece.

Let me talk a little about the mechanics of this piece. This piece is a standard verbogeometry piece so obviously I will be borrowing sections from my essay on verbogeometry to help open this up for you that are not familiar.

We all should be able to recognize a sphere, but did you know that a sphere has a relationship to the Pythagorean Theorem? To see this relationship we first should talk about the relationship between the distance formula and the Pythagorean Theorem. Then we will look at the relationship between the distance formula and a circle and after that the sphere. The distance formula uses the Pythagorean Theorem to calculate distances on the Cartesian coordinate system. The Pythagorean Theorem says that the square of the hypotenuse of a right triangle is equal to the sum of the square of it sides.

Solve for c and we get the following:


Let us look at little closer at how the Pythagorean Theorem works in a Cartesian coordinate system. Here is an example: Plot two points on a two-dimensional axis system P1(-9,10) and P2(4,3) and If we draw a lines between the points and lines parallel to the axes we can obtain a right triangle.

To solve the length of the hypotenuse we first find the difference between the x values and the y values to create the sides of the triangle then we plug the values into the Pythagorean Theorem. The x value is 9 - 4 = 5 and the y value is 10 - 3 = 7Now we plug it to the equation and we get the expression in the following figure:

The distance or length of the hypotenuse would be the square root of 74 or approximately 8.602

The distance formula in two dimensions is thus -- Given two points (x1,y1) and (x2,y2):

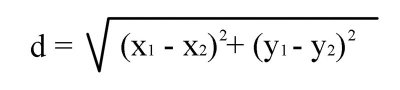To reiterate -- you will notice that the distance formula is nothing more than Pythagorean Theorem placed on a Cartesian coordinate system! The x1-x2 in our equation actually shifts the line horizontally and the y1-y2 shifts the line vertically. In effect if we start at the origin for our point (x1,y1) then we can simplify the equation as shown below:

Let us look at the equation for a circle: (below) --- Doesn’t it also look remarkably like the Pythagorean Theorem? In essence it is the Pythagorean Theorem! Notice that the radius of the circle corresponds to the hypotenuse of the right triangle. What we do is sort of ‘nail down’ one end of our right triangle at the hypotenuse and spin it around so that the other end of the hypotenuse follows the form of a circle.
All of the equations that we have been looking so far function in two dimensions but what if we wanted to use the Pythagorean Theorem in three dimensions? To use the Pythagorean Theorem or the distance formula in three dimensions we append another term at the end of the equation so it looks like the one below.

The Pythagorean Theorem in three dimensions is the same as it was in two dimensions except that we add another term at the end to give us the extra dimension.

Let us look at the equation for a sphere (below):

Notice that it looks just like the Pythagorean Theorem in three dimensions? It follows the same thought that we did in two dimensions. Where we ‘nail down’ one end of the triangle and spin it around in a circle but since we are in three dimensions, we also spin the circle around an axis and so it goes that the end of the triangle we started with now follows the form of a sphere.

This concludes discussing the analytic geometrical aspects of “The Virtuous Sphere” You can see that I used the equation for a sphere as my mathematical language for this piece. The only thing we haven’t discussed is the verbogeometric properties of the piece. The next entry in my blog will discuss some of the mechanics of verbogeometry that are needed to approach this piece.