Geof Huth's Mathematical Poetry # 2

Here is number two of Geof Huth’s mathematical poems.

Geof Huth's Mathematical Poetry # 1

I would like to share a series of mathematical poems by the Visual Poet Geof Huth. The next four days will be dedicated to this series. What I find interesting is that they are almost totally pure mathematical poems and not visual mathematical poems as such. This may surprise some because Geof is such a strong force in the visual poetry movement. These poems are so rich mathematically that making them work as mathematical visual poems would be extremely difficult. Geof tells me he plans to add visual poetic elements to these pieces so it will be interesting to see what he produces.

Golden Fear at Multiple Universes

Golden Fear has been accepted into the Multiple Universes show at the Poway Center for Performing arts in Poway California. The address is: 15498 Espola Road Poway, California -- tel (858) 748-0505

The show opens Sept 30, 2006 and closes Oct 30, 2006 the reception is Sunday afternoon at 2:00 PM Oct 8, 2006

Ancient Mathematical Visual Poem

JoAnne Growney has provided us with an ancient mathematical visual poem and its translation. A copy of the original manuscript can be seen above and at this URL here (click here). (Courtesy of ubuweb's early visual poetry page) The poem's explanation was difficult to find--but friend and colleague Sarah Glaz (Mathematics--University of Connecticut) tracked it down in Petrarch and the English Sonnet Sequence, by Thomas Roche, a book appearing in the bibliography of UBU's site of the Lok's poem. Oh ... and check out the square poems on JoAnnes website!

The translation is below:



Here we have a text interpretation of the manuscript photo, on page 166 of Petrarch and the English Sonnet Sequences by Thomas P. Roche, Jr. New York: AMS Press, 1989). In an Appendix on page 549, Roche also provides the text of two Latin mottos that surround the square. I have placed these at the top and at the bottom. Roche’s Appendix G goes on to point out the complexity of the structure within the square. For example, five lines The actual structure of this square poem is quite a bit more complex than the square itself.
For example, the columns down from E and F read:
God makes kings rule for heaue[n]s; your state hold blest
And still stand will their shields; fear yields best rest. [Roche, p. 550]
Embedded in the poem also are other poems, found by tracing the patterns of other squares (for example the sequence 1, 2, 3, 4, 5) and also crosses (using the letters, A, B, C, D, E, and F as reference points—A, B, E, and F, designate columns, as shown below and C, D designate the 5th and 6th rows.

Friedrich Schlegel’s Mask of God

Marko Niemi has translated Friedrich Schlegel’s mathematical poem for us. Marko also poses the question what happens if you divide the God by zero one more time.
I would love to hear Paul Gailiunas expound on that question. I think he would shy away from the idea of exploring the idea of God divided by zero but he may give us an answer to what happens when you divide infinity by zero.

Earliest Mathematical Poem?

Marko Niemi just sent me this link: (click here) …It looks very interesting! ... unfortunately I can not read German. Maybe someone will translate this for us. Marko tells us it was written by the German philosopher Friedrich Schlegel in the 19th century. Even though I can not translate it, I do know the beauty of dividing by zero. Although mathematically dividing by zero is undefined, the limit as you reach zero approaches infinity. In other words if you graph 1/x you can see the asymptote blow up in your face right at zero and it is a wonderful sight!

It is also interesting to see how artists gravitate toward dividing by zero. An example of this beauty can be seen in the taoist poem above by Karl Kempton.

Here is another thought on dividing by zero

Marko just sent me a translation of Schlegel's poem I will show it in the next blog entry

Here is a link to the translation: click here

Miscellaneous Mathematical Visual Poetry Links

Stratigraphy and Significance in the Fibonacci Sequence

click on the word algebraic

Mathematical Poetry Visual and Verbal

MNMLST POETRY: Unacclaimed but Flourishing

Bridges 2006 Abstracts

Bridges Conference on Mathematical Connections in Art, Music and Science starts Aug 2 2006 --- Click Here to list the Abstracts for the 2006 proceedings.

Bernar Venet

I had mentioned that Bernar Venet influenced me in the late 1970's. I have always enjoyed his work. I found a very nice essay about Venet by the Mathematician Karl Heinrich Hofmann. What I liked the most about this essay is its illumination of the fact that Venet does not present math as art but math as it is. However, the context in which Venet displays his work is in an art gallery or museum.

Click here for the essay

Karl Kempton Links

The Mathematical Visual Poetry of Karl Kempton links:
Revista de Poesia

M is for Mathematica

Runes about Karl's runes by Karl Young

The Root of Pi

Mathematical Poetry links:

Buddhist Mathematics

My Big Mouth

Mouth

Dusk

Six Alone In

Zen Poems

About Karl Kempton:

dbqp

North America's Longest Running Visual Poetry Magazine Edited by Karl Kempton, Harry Polkinhorn, and Karl Young -- Kaldron

Critical writings of Karl Kempton:

VISUAL POETRY: A Brief History of Ancestral Roots and Modern Traditions

CARRYING POETRY INTO THE 21ST CENTURY

Centered in London

My piece “Centered” was accepted in the Bridges Exhibit of Mathematical Art.

There is a lot of very interesting Mathematical Art in the Show Check out the other Art at the following link.

Righteousness

I have always found Mytho-spiritual aphorisms to be beautiful and every time I discover a new one if feel my life has new depth. They seem to me to be the archetypical fabric in all mythologies / religions as I have found them to be translatable and transmutable between the myths. I have also found that translating them into the language of math to be aesthetically rewarding. The piece righteousness above is one such aphorism which basically states that the more you display righteousness the less you really have. Of course this aphorism can be said for many disciplines for it seems we have all experienced the braggart who is more interested in covering his insecurities than setting an example for us to follow.

The equation is 'D' is proportional to 1/r ... or in otherwords 'D' is inversely proportional to r

New/Old Math Humor

I don't know where this came from but it reminds me of the logic used by a mathematical poet I know.

click here for the video

Early Karl Kempton visual poetry (plotter poems)

Here we have some interesting early visual poetry from Karl Kempton which used mathematical programing to plot these poems the link takes you to a page on Dan Wabers wonderful minimalist concrete poetry site. Here is the main page: minimalist concrete poetry

Mobius Poem by Endwar

Here is a link to a wonderful Mobius Poem by Endwar. Very Nice!
Click here for the Mobius Poem

Prometheus Epistle to Job

Do the muses scatter ancient fragments of thought or do they just perpetuate them. How is it that the ancient Greek Titans can still speak?

also see Orthogonal Space Poem

The Virtuous Sphere (part two)

The Virtuous Sphere (part two)
This blog entry is a continuation of “The Virtuous Sphere” please read the last blog entry so that today’s will make sense.

On the last blog entry, we had just finished talking about the equation of a sphere. However, the next question one may ask is, “why are there words in the equations instead of numbers?” To answer this question, you should read my essay on verbogeometry. I am going to republish some of the essay that relates to “The Virtuous Sphere” but if you have not read the essay on verbogeometry then you may not get as much out of this as you would if you were to read it.

Distance Formula and Verbogeometry: As we have seen, to calculate the distance between two points, we need to describe our points by its coordinates using the nomenclature of the coordinate pair. Let me reiterate, describing a point in verbogeometry is no different from numerical coordinates except we use words. Lets look again at the example in figure 15 where we used the midpoint formula to find the exact point between the points: P1(love,praise) and P2(hate,punishment) but instead of putting them in the midpoint formula lets put them in the distance formula. (See below)

Here we have an expression for the distance between the points P1(love,praise) and P2(hate,punishment) in two dimensions. But we can also use verbogeometry in any number of dimensions including hyper-dimensions. But before we look at hyper dimensional verbogeometry lets look at another example which we will express in the third dimension. The following example uses a three dimensional Cartesian coordinates system with 3 simple antonym word-axes. (See below) The first axis is noble / ignoble the second axis is just / unjust and the third axis is loyal / disloyal.
Now lets look at the expression for the distance between the points P1(noble,just,loyal) and P2(ignoble,unjust,disloyal) (see below)
Notice the green line in figure 33 is the visual representation for the mathematical expression above. However, it would be much easier to visualize if we were able to rotate the axis. Figure 33 is an isometric view, which I chose to use because it is best for viewing the axis but unfortunately at the expense of viewing the spatial orientation of the green line.

(The virtuous sphere is written in the language of three dimensions. What I find interesting is that we can write a spherical equation in hyper dimensions. The following shows the distance formula written in a hyperdimension.)

Now let us look at verbogeometry in a hyper-dimension. Let us look at the distance formula used in seven dimensions:Figure 35 shows the mathematical poem 1+1+1+1+1+1+1+1 =1 This is a metaphorical piece that creates a metaphoric path from the concept of confusion, to where seven deities meet. The piece uses the analytic geometry distance formula in a seven dimensional space where each dimension is a gradation from confusion to a point where a deity exists.

Here is a detail:

Lets look at the coordinate pairs for these two points P1(confusion, confusion, confusion, confusion, confusion, confusion, confusion) and P2(Allah,Buddha,Jesus,Spider woman,Vishnu,Yahweh,Zeus)

The Virtuous Sphere (part one)

The Virtuous Sphere (part one)

I thought it would be a nice idea to post "The Virtuous Sphere" and talk some about it. First of all I would like to say that I believe there are many ways to define virtue, this is only an artist rendition of one way. Please do not get bound up here in the idea of some absolute truth… remember the Hindu saying: “All wars are Just on both sides” When this piece was originally mediated to me my intentions were not so much interested in an answer of denotation but in the aesthetic inherit with the structure of a mathematical sphere and the coloration and distortion of that sphere by the personal ideas of integrity, justice, nobility and of course virtue.

Today's blog entry will talk about the analytic geometry involved in the piece and the next blog entry will discuss the verbogeometrical ideas needed to approach this piece.

Let me talk a little about the mechanics of this piece. This piece is a standard verbogeometry piece so obviously I will be borrowing sections from my essay on verbogeometry to help open this up for you that are not familiar.

We all should be able to recognize a sphere, but did you know that a sphere has a relationship to the Pythagorean Theorem? To see this relationship we first should talk about the relationship between the distance formula and the Pythagorean Theorem. Then we will look at the relationship between the distance formula and a circle and after that the sphere. The distance formula uses the Pythagorean Theorem to calculate distances on the Cartesian coordinate system. The Pythagorean Theorem says that the square of the hypotenuse of a right triangle is equal to the sum of the square of it sides.

Solve for c and we get the following:


Let us look at little closer at how the Pythagorean Theorem works in a Cartesian coordinate system. Here is an example: Plot two points on a two-dimensional axis system P1(-9,10) and P2(4,3) and If we draw a lines between the points and lines parallel to the axes we can obtain a right triangle.

To solve the length of the hypotenuse we first find the difference between the x values and the y values to create the sides of the triangle then we plug the values into the Pythagorean Theorem. The x value is 9 - 4 = 5 and the y value is 10 - 3 = 7Now we plug it to the equation and we get the expression in the following figure:

The distance or length of the hypotenuse would be the square root of 74 or approximately 8.602

The distance formula in two dimensions is thus -- Given two points (x1,y1) and (x2,y2):

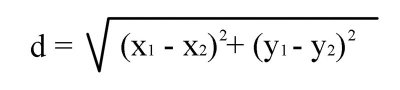To reiterate -- you will notice that the distance formula is nothing more than Pythagorean Theorem placed on a Cartesian coordinate system! The x1-x2 in our equation actually shifts the line horizontally and the y1-y2 shifts the line vertically. In effect if we start at the origin for our point (x1,y1) then we can simplify the equation as shown below:

Let us look at the equation for a circle: (below) --- Doesn’t it also look remarkably like the Pythagorean Theorem? In essence it is the Pythagorean Theorem! Notice that the radius of the circle corresponds to the hypotenuse of the right triangle. What we do is sort of ‘nail down’ one end of our right triangle at the hypotenuse and spin it around so that the other end of the hypotenuse follows the form of a circle.
All of the equations that we have been looking so far function in two dimensions but what if we wanted to use the Pythagorean Theorem in three dimensions? To use the Pythagorean Theorem or the distance formula in three dimensions we append another term at the end of the equation so it looks like the one below.

The Pythagorean Theorem in three dimensions is the same as it was in two dimensions except that we add another term at the end to give us the extra dimension.

Let us look at the equation for a sphere (below):

Notice that it looks just like the Pythagorean Theorem in three dimensions? It follows the same thought that we did in two dimensions. Where we ‘nail down’ one end of the triangle and spin it around in a circle but since we are in three dimensions, we also spin the circle around an axis and so it goes that the end of the triangle we started with now follows the form of a sphere.

This concludes discussing the analytic geometrical aspects of “The Virtuous Sphere” You can see that I used the equation for a sphere as my mathematical language for this piece. The only thing we haven’t discussed is the verbogeometric properties of the piece. The next entry in my blog will discuss some of the mechanics of verbogeometry that are needed to approach this piece.

A Screening of Super-8 films by Robert C. Morgan

I studied with Robert C. Morgan in the late 1970’s and he is responsible for much of my earlier artistic development. He exposed me to the conceptual art movement in general and Benar Venet in particular. Venet noticed that science had aesthetics as well as art and was bold enough to re-contextualize these scientific aesthetics as Art. It wasn’t until I read the Dancing Wu Li Masters by Gary Zukav that I experienced an epiphany that drove me into mathematics and science. Prior to that event I had no interest in mathematics and some disdain. However, I must say I loved math up until I was seven years old then, as I mentioned, I abandoned it until 1979.
Robert has always been supportive and I always wish the best for him.

Millennium Film Workshop

presents


A Screening of Super-8 films by Robert C. Morgan

Saturday, June 17, 2006, at 8 PM



Although known today primarily as a critic and curator, Robert Morgan
emerged as a "post-conceptual" artist in the mid-seventies. Between 1974 -1989,
Morgan worked in a variety of different media, including an extensive body
of work in Super-8 film. He regards his films as "counter-narrative" in that
they deconstruct both Hollywood and commercial television -- the two primary
forms of visual narrative in the entertainment industry -- by laminating appropriated
footage against a personal and often political narrative. This is a rare opportunity
to see films by one of the formative "appropriation" artists of the seventies.

A reception will precede the screening in the Millennium Gallery at 7 PM

Admission: $8 / $6 (members)


For further information, please contact:

Millennium Film Workshop
66 East 4th Street, NYC 10003
Tel & Fax: (212) 673 - 0090
Email: cinema@millenniumfilm.org

The Transformation of Poison

The image above has been simmering in the background for a few years now and has finally come to fruition. It came about in December 2001 over a cup of coffee while taking a break at the ASCI conference in NYC. At the conference I met a very interesting Poet/Artist Philosopher and NASA scientist named Farzad Mahootian. We had a wonderful conversation between sips of dark java in mid town Manhattan and talked of many things. I shared my ideas on verbogeometry while he shared his ideas on sculptures that purify the environment. In our mutual excitement he thought it would be a good idea to incorporate the two ideas into a piece of Art. The piece above is the result. I decided to make a symbolic wedge from a verbogeometric prism and have it cleaning the air with chrysanthemum power.