Factorial By Scott Glassman

i
am a
quotient of the

sun
i am
a quotient of

the
moon i
am a quotient

of
the one
i am a

quotient
of the
two i am

a
quotient of
the burn i

am
a quotient
of the dew


2.

i
am a
multiple of the

earth
i am
a multiple of

the
sea i
am a multiple

of
the birth
i am a

multiple
of the
tree i am

a
multiple of
the word i

am
a multiple
of the air


3.

i
subtract myself
from you for

luck
i add
myself to you

for
love i
subtract myself from

you
for luck
i add myself

to
you for
love i subtract

myself
from you
for luck i

add
myself to
you for love


4.

i
am zero
over you +

1
i am
zero over you

+
2 minus
0 over you

+
1 minus
0 over you

plus
2 minus
you over me

+
0 minus
1 over you

The poem above is a poem by Scott Glassman called factorial taken from his blog.

I find this poem of Scott Glassman very interesting in that I can see it as an example of mathematical poetry buried inside mathematics poetry. (Click here for the difference between mathematical poetry, mathematics poetry and mathematical visual poetry) The first section of Scott’s poem I have transformed into a piece of mathematical visual poetry. (above) This mathematical visual poem shows four separate mathematical poems that are contained within section one of his mathematics poem.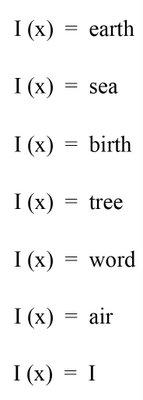



The verses in the second section have different meanings dependent on whether the poem is lineated or written without lineation. However, both ideas are present in the poem. You can feel the tension between differing statements and the shift in context between the statements due to reading it lineated and then reading it not lineated. I have written out all the mathematical poems/verses I could find contained within this section and displayed them in the image shown above.



The third section functions much the same as the second as far as tension between lineation and reading it without the lineation. However this section has only two statements repeated three times. The interesting part in this section is that the lineation creates two more mathematical poems which are shown in black (above).



The fourth section is a bit more difficult to map out. Therefore I shot a photo of my deductions from the poem. (above) You can see the brackets point to three mathematical poems that are delineated by the brackets inside the mathematics poem. The third one of the three I used algebra to simplify the expression into a compact form/context. Watch the meaning change in this poem through all the metamorphoses.

Geof Huth Mathematical Poetry Links

This page is reserved for Geof Huth's Mathematical Poems and related material

Algebraic Poem #1

Algebraic Poem #2

Algebraic Poem #3

Algebraic Poem #4

Mathematical Graffiti

art@IIT Upcoming Show

Anonouncing the upcoming show art@IIT currated by my friend Robert Krawczyk

Introduction To ‘Visual Mathematical Poetry’

"Americana Mathematics" (above)

-Details Views (below)-

Introduction to ‘Visual Mathematical Poetry’:
I would like to introduce another category for mathematical poetry related nomenclature. This delineation I would like to call visual mathematical poetry. This is a mathematical poem where the elements in that poem are visual objects. The difference between mathematical poetry and visual mathematical poetry is that the former uses words and the later uses images. Visual mathematical poetry is more similar to mathematical poetry than it is to mathematical visual poetry. However, one could create a poem that has aspects of all three of these types. There are plenty examples of math type poems out there that use elements of visual mathematical poetry however, I have seen none that are done with the intent of having a didactic element within them and most if not all are too abstract to show the mechanics of visual mathematical poetry. Furthermore, I have not seen any that are ‘purely visual mathematical poetry to serve as clear example.
Verification of logic:
I have tested the logic in this piece on a group of aerospace engineers to see if the artistic aesthetic interfered with the logic. All of them clearly saw the logic and understood the mechanics of the piece however, a couple asked, in perfect stereotypical engineering demeanor, why would I bother.
I also presented this to the mathematician Paul Gailiunas who replied below:
"It goes further - there are special numbers if we do multiplication (the primes), but none in addition. Number theory follows. We can set up other systems that work like this, but the elements need not be numbers. They are called rings. Division is a further complication. Sometimes it works, and we have a "division ring", sometimes it doesn't. The integers do not form a division ring because things like 2/3 are not integers."
The mechanics of this piece:
What motivated this piece was some conversations with a few people who have trouble visualizing mathematical poetry in general and the difference between addition and multiplication in particular. I decided to create this piece to possibly help those people approach this nebulous concept. For if we look at addition we see 2 concepts put together in such away that the original concept is easy to remove from the other and both concepts are easy to identify retain their original identity. I think most people do not have much of a problem comprehending this idea. However, multiplication is much trickier to embrace. Using the operation of multiplication augments the result by integrating the identity of both elements being multiplied. That is in the example of 4 x 5 = 20. ‘Twenty’ can be seen to have been augmented by both 4 and 5 and one can see this by dividing up 20 by cutting out 5 pieces of 4 or 4 pieces of 5. What is important is that we recognize that 20 is a higher magnitude relative to both 4 and 5 but has the ‘identity’ of both 4 and 5. “Americana mathematics” operates the same way for in addition one can easily recognize and conceptually separate both identities. Furthermore, the multiplication operation has a result that is an augmentation of both separate identities but obviously is more powerful than the original ideas, has its own identity however; it retains the original identities of both.

For a web page version click here

Perelman and Me

Here is a timely mathematics poem by JoAnne Growny:



Perelman and Me

On Tuesday, August 22, 2006 Russian mathematician Grigory Perelman declined the Fields Medal for his contribution to the proof of a well-known and difficult conjecture first posed by Henri Poincare in 1904. I applaud Perelman’s seclusion.


The gravity of the universe
requires dark matter.
Choosing one thought
prevents another.

Little girls learn social graces
to make others feel at ease.
But friendly greetings
are never mathematics.

Difficult thoughts
are born in isolation :
genius slips away if socialized—
and so he must refuse the prize.

JoAnne Growney
25 August 2006

Why I Don’t Want To Teach (Math Joke#4)

Grumman on Schlegel

Bob Grumman has just posted Marko Niemi’s translation of Friedrich Schlegel’s equation for poetry and God on his blog at this URL: click here

Bob has made the following comments:

“This is a translation by Marko Niemi of the 19th-Century German philosopher Friedrich Schlegel’s formula for poetry. Kaz thinks it may be the world's first mathematical poem. I'm not sure. It seems mostly informrature to me--i.e., intended to inform rather than provide beauty, as literature is intended to do (in my poetics). It is a way of mathematically defining something philosophical as e equals mc squared mathematically defines energy, rather than creating a poetic experience. It is entirely asensual--at least for one like me, who has no notion what material feature "God" has. Mathematically, it is a little silly, too--for if "shit" were substituted for "FSM," the equation would be in no way altered. On the other hand, it is a marvelously step toward what Kaz and I and Geof and Karl are doing, perhaps a pivotal one (although I don't know of anyone who was inspired to create mathematical poetry by it).”

I would like to address a few things from his comments.

Bob says, “Kaz thinks it may be the world's first mathematical poem. I'm not sure.”

I would like to note that I doubt that this poem was the first mathematical poem ever written. It is however the earliest mathematical poem that I have seen. I have seen earlier mathematical visual poems but no mathematical poems this early. For an understanding of the difference between mathematical poem and mathematical visual poem, please check my terminology at this link: click here

Bob says, “It seems mostly informrature to me--i.e., intended to inform rather than provide beauty, as literature is intended to do (in my poetics).”

I see this as expressive rather than informative. The question to ask is, “Was Schlegel’s equation meant to be denotative or connotative. It is hard if not impossible to be denotative when you are dividing by zero. Concerning aesthetics, Bob has a very different idea of beauty than I and his views of mythology are very different from mine as well. Bob is certainly entitled to his opinion. Although I also would have to say that Schlegel’s view of God is about as different to my view as mine is to Bob’s. I think the main aesthetical point to Schlegel’s poem is tying “The Transcendent” to an expression of infinity … not just once but six times. There are many things beautiful to mathematicians and infinity is definitely one of them if not the greatest idea of beauty. On the other hand, those who believe in “God” would also believe that the idea of God is the greatest beauty. However, I am certain that my idea of God is heretical to those same believers, for I do not believe in using lower case letters for the ‘G’ in God. All Gods are metaphors to The Transcendent.

Bob says, It is a way of mathematically defining something philosophical as e equals mc squared mathematically defines energy, rather than creating a poetic experience.

Here Bob equates philosophy with science … That was certainly true in 300 BC. However, there is nothing scientific about this equation for a scientist in Schlegel's time would never divide by zero (it is undefined for scientific use but perfect for poetry in fact it is the crux of metaphor)
Here is Schlegel’s view:
“Schlegel argued that poetry should be at once philosophical and mythological, ironic and religious. As a literary critic Schlegel sought not to reveal objective truths, but to write criticism so that the usual discursive prose becomes a work of art itself.” **

Bob says, It is entirely asensual--at least for one like me, who has no notion what material feature "God" has.

I am confused … I do not know where ‘anything’ physical was stated or implied.

Bob says, Mathematically, it is a little silly, too--for if "shit" were substituted for "FSM," the equation would be in no way altered.

The latter statement is another aesthetic judgment and again Bob is entitled to any scatological view he desires ;)

Bob says, On the other hand, it is a marvelously step toward what Kaz and I and Geof and Karl are doing, perhaps a pivotal one (although I don't know of anyone who was inspired to create mathematical poetry by it).”

If Schlegel inspired anyone to write mathematical poetry then Marko Niemi may be the closest person to know for he is our source.


**The quote was taken from this web site: click here

Emerson Quote #2

Karl Kempton sent us this Emerson Quote:


Every word was once a poem.

-Ralph Waldo Emerson, writer and philosopher(1803-1882)

Emerson Quote #1:

Language is fossil poetry.

Ralph Waldo Emerson, writer and philosopher (1803-1882)

The Biggest Problem To Overcome With Math-Art

Waterfall by M. C. Escher 1961

The biggest problem to overcome with math-art in general is that it is tied to two mutually exclusive aesthetic ideas. One idea being that pure mathematics pervades all cultures. The second is that Art is the expression of a particular culture. Math being the language of logic shares the same logic in France as it does in China. Art may express an archetype but the ‘expression’ is cultural. I believe these two ideas are true in a broad sense although there is a little room for argument in the finer details.
I feel that using math as a language for art demands that the mathematical expression or structure has to have some relationship to the cultural idea put forward. There is much mathematical art expressed which is beautiful from a mathematical perspective but trivial from an art perspective. Furthermore, the converse of this is true as well. There is mathematical art that artists may find beautiful however, evokes yawns from the mathematics community.
I think the measure of success of any mathematical art lies in how well it is accepted by both communities. This is a very difficult task and there is a plethora of work accepted by one community but not the other. I think the most successful artist that is accepted by both communities is M C Escher. Even though his acceptance is expressed more by the math community than the art community this cannot be helped. Finding the middle ground would be near if not impossible. At the other end of the spectrum, I am going to risk saying that I believe you are delusional if you believe you have made great math art/poetry and you are accepted by only one community no matter how much croaking the one community does.

Why I Don’t Want To Teach (Math Joke#3)

Why I Don’t Want To Teach (Math Joke#2)

Hyper-Dimensional Poetry?

When I was first introduced to hyper-dimensional geometry I was quite fascinated but really didn’t have any clear path to understand it. I had seen two dimensional images of a hypercube (four-dimensional cube) but really understood nothing about what I was looking at. With computer imagery we are able to see things a little better because we can simulate three-dimensions in a video or other moving imagery. The following link will take you to a polytope slicer which allows you to take three-dimensional slices through a four-dimensional object.
Let me expound upon this a little bit. Just about all of us have experienced slicing a near two-dimensional piece of paper with a pair of scissors. When we do this we experience seeing a near one-dimensional line at the edge of the paper where we just cut. Many of us have also experienced slicing a ‘three-dimensional’ orange in half and noticing a two-dimensional surface showing the cells inside the orange. However things get a little trickier when we slice a four-dimensional object. If you notice on our previous examples that the slice is a dimension less than the object we started with. That is a slice of a three dimensional object is two-dimensional and a slice of a two-dimensional object is one dimensional. Therefore, to imagine a slice of a four-dimensional object our result would be something that has three-dimensions. Our polytope slicer does just that! It gives us a three dimensional-section cut of a four-dimensional regular polytope. Your next question may be, “what is a polytope?” A polytopes are to four dimensions as polyhedrons are to three dimensions or what polygons are to two dimensions.

As you vary the parameters in the polytope slicer you will get three-dimensional slices of our four-dimensional polytope. (click here for the polytope slicer).

Now what does this have to do with mathematical poetry? All maths can be used as language for poetry. Use your imagination … I predict that someone will write a poem on a hypercube so that we can read it by projecting it down to the third dimension. This may have already been done but I am not aware of it. After one does it with a hypercube then try doing it on a 120 cell hyperdodecahedron or maybe an epic poem on a 600 cell hypericosahedron

Why I Don't Want To Teach (Math Joke#1)

Here is a math joke sent to me by Aerospace engineers Paul Mossel and Keith Rowley on the subject of why I don’t want to teach.

Geof Huth's Mathematical Poetry # 4

Here is the last of Geof’s Poems from this group. I find it wonderful to see other people making these types of mathematical poems. I especially enjoy this form with a series of poems building a context from which we can stand. Thanks Geof for sharing these with us!

Geof Huth's Mathematical Poetry # 3

I would classifiy the poem above as a pure mathematical poem except for one small element that I would classify as mathematical visual poetry ... can you find it?

Geof Huth's Mathematical Poetry # 2

Here is number two of Geof Huth’s mathematical poems.

Geof Huth's Mathematical Poetry # 1

I would like to share a series of mathematical poems by the Visual Poet Geof Huth. The next four days will be dedicated to this series. What I find interesting is that they are almost totally pure mathematical poems and not visual mathematical poems as such. This may surprise some because Geof is such a strong force in the visual poetry movement. These poems are so rich mathematically that making them work as mathematical visual poems would be extremely difficult. Geof tells me he plans to add visual poetic elements to these pieces so it will be interesting to see what he produces.

Golden Fear at Multiple Universes

Golden Fear has been accepted into the Multiple Universes show at the Poway Center for Performing arts in Poway California. The address is: 15498 Espola Road Poway, California -- tel (858) 748-0505

The show opens Sept 30, 2006 and closes Oct 30, 2006 the reception is Sunday afternoon at 2:00 PM Oct 8, 2006

Ancient Mathematical Visual Poem

JoAnne Growney has provided us with an ancient mathematical visual poem and its translation. A copy of the original manuscript can be seen above and at this URL here (click here). (Courtesy of ubuweb's early visual poetry page) The poem's explanation was difficult to find--but friend and colleague Sarah Glaz (Mathematics--University of Connecticut) tracked it down in Petrarch and the English Sonnet Sequence, by Thomas Roche, a book appearing in the bibliography of UBU's site of the Lok's poem. Oh ... and check out the square poems on JoAnnes website!

The translation is below:



Here we have a text interpretation of the manuscript photo, on page 166 of Petrarch and the English Sonnet Sequences by Thomas P. Roche, Jr. New York: AMS Press, 1989). In an Appendix on page 549, Roche also provides the text of two Latin mottos that surround the square. I have placed these at the top and at the bottom. Roche’s Appendix G goes on to point out the complexity of the structure within the square. For example, five lines The actual structure of this square poem is quite a bit more complex than the square itself.
For example, the columns down from E and F read:
God makes kings rule for heaue[n]s; your state hold blest
And still stand will their shields; fear yields best rest. [Roche, p. 550]
Embedded in the poem also are other poems, found by tracing the patterns of other squares (for example the sequence 1, 2, 3, 4, 5) and also crosses (using the letters, A, B, C, D, E, and F as reference points—A, B, E, and F, designate columns, as shown below and C, D designate the 5th and 6th rows.

Friedrich Schlegel’s Mask of God

Marko Niemi has translated Friedrich Schlegel’s mathematical poem for us. Marko also poses the question what happens if you divide the God by zero one more time.
I would love to hear Paul Gailiunas expound on that question. I think he would shy away from the idea of exploring the idea of God divided by zero but he may give us an answer to what happens when you divide infinity by zero.

Earliest Mathematical Poem?

Marko Niemi just sent me this link: (click here) …It looks very interesting! ... unfortunately I can not read German. Maybe someone will translate this for us. Marko tells us it was written by the German philosopher Friedrich Schlegel in the 19th century. Even though I can not translate it, I do know the beauty of dividing by zero. Although mathematically dividing by zero is undefined, the limit as you reach zero approaches infinity. In other words if you graph 1/x you can see the asymptote blow up in your face right at zero and it is a wonderful sight!

It is also interesting to see how artists gravitate toward dividing by zero. An example of this beauty can be seen in the taoist poem above by Karl Kempton.

Here is another thought on dividing by zero

Marko just sent me a translation of Schlegel's poem I will show it in the next blog entry

Here is a link to the translation: click here

Miscellaneous Mathematical Visual Poetry Links

Stratigraphy and Significance in the Fibonacci Sequence

click on the word algebraic

Mathematical Poetry Visual and Verbal

MNMLST POETRY: Unacclaimed but Flourishing

Bridges 2006 Abstracts

Bridges Conference on Mathematical Connections in Art, Music and Science starts Aug 2 2006 --- Click Here to list the Abstracts for the 2006 proceedings.

Bernar Venet

I had mentioned that Bernar Venet influenced me in the late 1970's. I have always enjoyed his work. I found a very nice essay about Venet by the Mathematician Karl Heinrich Hofmann. What I liked the most about this essay is its illumination of the fact that Venet does not present math as art but math as it is. However, the context in which Venet displays his work is in an art gallery or museum.

Click here for the essay