Verbogeometry -- installment II --- Word-Axes and Word-Planes
2. The Mechanics of Verbogeometry:
2.1. Word-Axes and Word-Planes. One of the tenets of Verbogeometry and Mathematical poetry is that you "calculate" values of quality as if they were quantity. Of course this seems to be nonsense but then one must realizes that paradox is the mathematical structure of metaphor. When quality and quantity are synonymous then the math equations automatically transcend the normal duty of denotation and enter into the realms of connotation. This concept also bears some relationship to different concepts of infinity pioneered by the Russian-German Mathematician Georg Cantor, namely the infinities in gradation relative to the infinities in Counting.
Another tenet of verbogeometry is that it recognizes antonyms in only a few varieties. A simple antonym is a word whose antonym is a direct negation. (Example: just / unjust, probable / improbable or fertile / infertile etc.) A complex antonym is a word whose antonym is not a direct negation. (Example: just / unfair, probable / doubtful or fertile / barren etc.) There are also gradable (gradient) antonyms which are pairs that express relationships in a continuum, such as up and down. Complementary antonyms are pairs that express an either/or relationship, such as dead or alive. Verbogeometry uses all antonyms as if they were gradable. It is easy to find examples where poets use complementary antonyms as if they were gradable to create certain metaphors. Example: "Bob showed up half dead to work today."
Within the boundaries of verbogeometry is important to understand that we view words as objects floating in space. When we focus on single words, with no context, they are alone inert relating to no other words. However, when we focus on words that have a synonymous partner we can easily imagine a line in space between the words. Probable and improbable are good examples of simple antonyms that we can view connected by a line. (See figure. 3)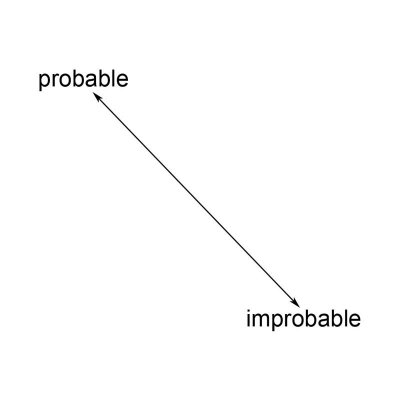
Figure 3.
Life is full of dualities it is hard to think about qualities without thinking about opposing ideas. We can view our 'probable / improbable' one-dimensional line as a number line but instead of values of numbers on the line, we think in terms about having different levels of meaning between the two words residing at each end of the line. Due to a number-line being a one dimensional axis it is easy to visualize a word-axis as an axis for a single spatial dimension. We call any pair of words connected by a line a word-axis. Two perpendicular number lines or word axes make a two-dimensional word-axis as well as defining a word-plane. We also have the ability to view the word-plane as an infinite number of coordinates delineated by the word-pairs much like the infinite number of coordinate pairs contained within a Cartesian coordinate system described in the realm of analytic geometry.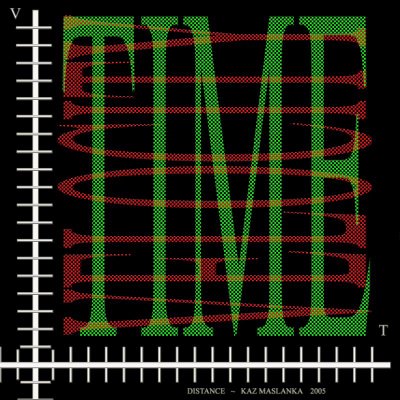
Figure 4.
Figure 4 shows a visualization for the physics equation; distance = velocity multiplied by the time. Notice that the y axis displays velocity and the x axis displays time. When we multiply and blend the words in an infinitesimal weave, we arrive at the concept of distance in a tessellated product of the concepts of velocity and time. In another words by positioning the two axes perpendicular to each other, we view every value on one word-axis in relation to every value on the other word-axis. This method affords us a way to 'feel' the entire word plane or axis system with all its different augmented values and gradations. When we multiply two word-axes together we conceptually tessellate a two dimensional plane with different semantic values of the two words blended and augmented. If we were to take a normal Cartesian coordinate system and multiply the x positive integers (1 through 12) times the y positive integers (1 through 12) we get a tessellated plane as in Figure 5 (see figure. 5) (notice the intensity of blue relative to the value of the numbers)
Figure 5.
To help us further visualize this concept let us create a word axis using the words red and green. In this instance, we are going to use red and green as nouns instead of adjectives. (We will use colors as adjectives later) Let us multiply a red-green axis times another red-green axis and view it visually. (See figure. 6) Multiplication of colors is similar to color addition except the disparate intensities of the colors are greater and follow a similar pattern shown in figure 5. The value of the 'numbers' is subjective and not as important as the relationship between the 'numbers'.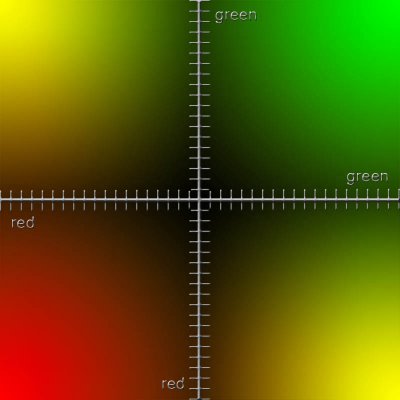
Figure 6.
Figure 6 helps us to visualize different word meanings spread across a word plane.
Let us create another example using two different word-axes. However, let's use two different colored word axes instead of both axes being the same colors like our previous example. Then let us break down what we have just accomplished and look at the axes separately. After that we will superimpose a set of different word-axes upon our color axes to compare how the system works.
To facilitate visualizing two different word axes lets look at an example with the word-axes red-green and blue-orange multiplied by each other and mapped on a Cartesian coordinate system. (See figure. 7)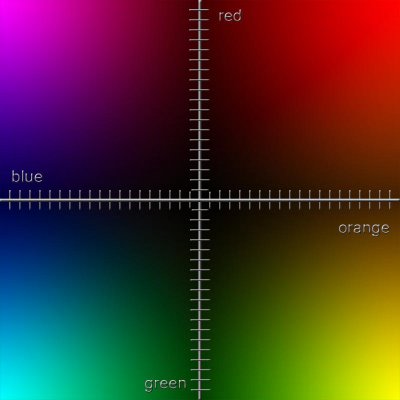
Figure 7.
(Note these diagrams are visual aids not scientific data)
Figure 7 is comprised of two axes: a red-green in the vertical and a blue orange in the horizontal. Let us look at the red-green vertical axis separately (See figure. 8)
Figure 8.
and separate the blue-orange horizontal axis as well (See figure. 9)
Figure 9.
Furthermore, notice the direction of the gradations. When we place the axes perpendicular to each other and multiply them together, we see the color tessellations of the word-plane. (See figure. 7)
What is nice about using colors for our examples is that words used for colors function as both a noun and an adjective depending on our intent. When we map a word plane with word-axes that comprise colors and we use them as adjective synonyms, then this word-plane serves as a paradigm or a pedagogical tool to serve as a general model for understanding all two axes synonym word-planes. Example: Let create a word-plane using the two word-axes of noble/ignoble and just/unjust. (See figure. 10)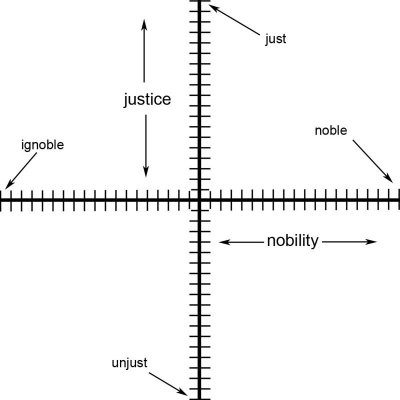
Figure 10.
The next step would be to superimpose the noble/ignoble; just/unjust word-plane onto our previous word-plane of blue/orange; red/green. In essence, we are pretending color blue to mean ignoble, orange to mean noble, red to mean just and green to mean unjust. Now we can see the meanings blend into each other in the different areas of our word-plane.(See figure.11)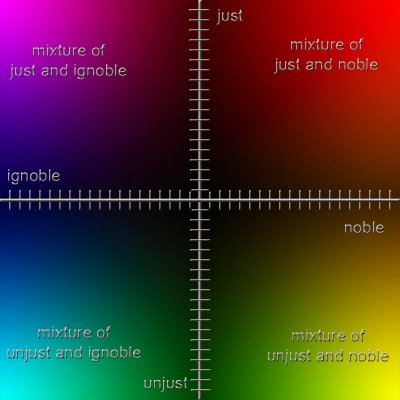
Figure 11.
We can see the color purple as blend of ignoble and just, red-orange as a blend of just and noble, yellow-green as a blend of noble and unjust and blue-green as a blend of ignoble and unjust. For the record, I certainly am not trying to say there is a relationship of ignobility and injustice with the color blue-green! This example is just a tool to help us with our own concept of visualizing a word-plane. However, we could create a different but, in my opinion, limited set of color metaphors for noble/ignoble and just/unjust. Or we could look at our color example as adjectives on their own merit. This method would automatically help us see them as metaphors. Example: She was red hot. He had a blue day. He was so green he did not know what was happening. Multiplying adjective word-axes together instantly create metaphors.
