Nokturno.org has a new fractal poem titled Palasista!
by Saara Lehto. The piece is written in Finnish and is in the form of a Sierpinski Carpet. The words are all anagrams of each other as well as the title.
Thanks to Marko Niemi for bringing this to us!
Gregory Vincent St. Thomasino has sent me a math poem that I would like to share with you.
to + to = too
This is a nice little poem that has three Important elements that strike me right off the bat:
1.) it plays on the words to and too … in other words we have too many to's
2.) is the clever addition of o's … o + o = oo
3.) the most important element of any mathematical poem is the equal sign.**
I really like the feeling in this piece … metaphor is so hard to describe without using another metaphor and if we do then we miss the point.
By the way … eratio seven is now available! Check it out!
** It is the equal sign that creates the metaphor in mathematical poetry. It is the fact that a poem of the latter form says a + b = c and we know that a + b IS NOT c
There exists a mathematical form that is the logical crux of all metaphors in all poetry mathematical or otherwise:
A = B
Given: We know for a fact that ‘A’ does not equal ‘B’
There is also one more key ingredient for metaphor to exist. That ingredient is connotative intention. In other words, the physics equation d = vt is not metaphorical because the intention of the equation is denotative.
‘A’ is similar to ‘B’ is not a metaphor
‘A’ is proportional to ‘B’ is not a metaphor
‘A’ looks like ‘B’ is not a metaphor
‘A’ is compared to ‘B’ is not a metaphor
Simile is not metaphor that is why they are different words
Karl Kempton shares some links with us:
Marius de Zayas, Agnes Meyer. Eye Contact: Modern American Portrait Drawings from the National Gallery, Nov 2005
Picabia. Between Music and the Machine: Francis Picabia and the End of Abstraction, fig 28 mathematical formulas. Nov 2005.
I really am not able to tell whether Zayas was trying to express something mathematically or not. I have seen an abundance of artists decorating their work with equations in order to express a math feeling or maybe add a cryptic quality to their works and that may be what Zayas is trying to do as well …These days the latter idea is a bit trivial however, the case with Zayas is probably one of the first times that equations are inscribed within visual work … (I wouldn’t put it past Hieronymus Bosch … but I don’t think he did it)
Thanks Karl for passing this on!
There are many who claim the endeavor of ‘mathematical poetry’ and we can see as many forms as there are claims. I personally see three different forms however, the second category I describe may be broke into many other forms. I will list them in order of popularity at this time in 2006. I also want to mention that I am not one to engage in taxonomy for taxonomy’s sake but delineate things only if I feel there is confusion. There also can be works that incorporate all three categories.
1. ‘Mathematics poetry’ -- This poetry is traditional language poetry about or inspired by mathematics. I also would consider poetry that plays with numbers and words in this category. There are numerous examples all over the web but the most popular from my perspective is Marion Cohen:
Another source would be Katherine Stange:
2. ‘Mathematical Visual Poetry’ – This is more difficult to define because of the vast areas and the many competing definitions of visual poetry. However, I consider mathematical operations on text as well as mathematical textual information composed for aesthetic purposes to be ‘Mathematical Visual Poetry’ Also words, text or textual elements mixed with mathematical symbols or formulae that are not performing mathematical operations on the words. Although Karl Kempton has worked in all three categories, I feel the following is a good example of ‘Mathematical visual poetry’: Another good example is Marko Niemi’s fractal poem described in the following link: Midwinter nights dream
3. ‘Mathematical Poetry’ – This is literally performing mathematical operations on concepts whether they are words or images. A good example would be my page at the following link: Mathematical Poetry
Also the following link has an example of Scott Helmes: And Bob Grumman at the following link is a good example of a mixture of ‘Mathematical Poetry and Mathematical Visual Poetry’:
Marko Niemi's Mathematical Visual Poetry:
Midwinter nights dream
http://www.nokturno.org/marko/haynaku/midwinter.html
The link above is my personal favorite of his and you can read my little essay about it click here
Fibonacci visual poem
http://www.nokturno.org/marko/nurotus/fibonacci/
The following is a Finnish visual poem based on the Sierpinski triangle
Kolmioita
http://www.nokturno.org/marko/nurotus/kolmioita/kolmioita.gif
Brownian motion series
http://www.nokturno.org/marko/brown/
"Eloquent Fern"
http://www.nokturno.org/marko/fern.html
The following statement is Marko's preface for the "Eloquent Fern"
The "text" in this piece is the following paragraph from "Rhetoric" by Aristotle, "translated" into four-letter DNA code: (It is clear, then, that rhetoric is not bound up with a single definite class of subjects, but is as universal as dialectic; it is clear, also, that it is useful. It is clear, further, that its function is not simply to succeed in persuading, but rather to discover the means of coming as near such success as the circumstances of each particular case allow. In this it resembles all other arts.)
Narcissus The series consists of six pieces, and in each piece, locations of individual letters are defined by the same polar coordinate function:RADIUS = A * cos(0.5 * ANGLE), where A is constant, and ANGLE goes from 0 to 720.The direction of each letter is independent from its location, but it's a function of ANGLE, too. This direction function is different in each piece, and it's the reason why pieces differ from each other, even though they all use the same location function.
Animated mathematical/scientific visual poems:
Critical Mass
Divine Intervention
Eye of the beholder
Party NRJ
I feel grateful to be a part of the vispo show in Cleveland Ohio this month the show is full of a lot of very talented artists. Check out the link below.
VISPO!
Blends & Bridges: A Survey of International Contemporary Visual Poetry & Related Art
Gallery 324 at the Galleria at Erieview is hosting a show of contemporary international visual poetry (Vispo for short).
The show is curated by Cleveland visual poet/publisher John Byrum, Florida visual poet/publisher Bob Grumman, and Cleveland artist Wendy Collin Sorin.
Gallery 324
1301 East Ninth Street
Cleveland, OH 44114
click here for show index
Fractal Visual Poetry
I want to get back to the fractal poem that was created by Marko Niemi and the post of mine from March 25th Midwinter night's dream (click here)
To understand some of the ideas incorporated into Marko’s piece we need to understand a little about this idea of fractals. Fractals have many facets of interest however; I want to focus on two:
1.) Self-similarity
2.) Fractional dimension
You may ask yourself, “Have I experienced a fractal in nature?” The answer is yes! I believe the easiest way to recognize that you have experienced one is by asking the question: “Have I ever noticed something that looks the same viewed at different scales: In another words the look very much the same whether I am close to it or far away.
Here is a short list of fractals patterns found in nature
*the branching of tracheal tubes
*the leaves in trees
*the veins in a hand
*galaxies
*water swirling and twisting out of a tap
*a puffy cumulus cloud
*tiny oxygen molecule, or the DNA molecule
*the stock market
*sea shells
I believe out of this list the easiest one to comprehend is a cumulus cloud. These kinds of clouds look the same from 60 feet away or 6 miles away. From either distance clouds basically have the same shape.
The picture below looks very much like the runoff from my neighbor’s water sprinkler before he got his Arizona lawn seeded properly.
But the fact is that I shot this photo of the Grand Canyon from one of my airplane flights between Denver and San Diego. Here we can see another self-similar example in the fact that water erosion looks pretty much the same from different scales.
Mathematical Fractals
We have all probably seen some ‘self similar’ mathematically created fractal images on the Internet or at a bookstore. However, to get a good understanding of it I wish to focus on the image below. The figure below is called a Sierpinski triangle named after the 20th century polish mathematician.
I don’t think that I could explain self-similarity any better than the following link so I stole the text “shown in red” from that site and posted it below:
http://math.bu.edu/DYSYS/chaos-game/node5.html
Self-similarity
One of the basic properties of fractal images is the notion of self-similarity. This idea is easy to explain using the Sierpinski triangle. Note that S may be decomposed into 3 congruent figures, each of which is exactly 1/2 the size of S! See Figure 7. That is to say, if we magnify any of the 3 pieces of S shown in Figure 7 by a factor of 2, we obtain an exact replica of S. That is, S consists of 3 self-similar copies of itself, each with magnification factor 2.
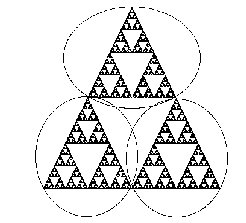
Figure 7: Magnifying the Sierpinski triangle
We can look deeper into S and see further copies of S. For the Sierpinski triangle also consists of 9 self-similar copies of itself, each with magnification factor 4. Or we can chop S into 27 self-similar pieces, each with magnification factor 8. In general, we may divide S into 3^n self-similar pieces, each of which is congruent, and each of which may be maginified by a factor of 2^n to yield the entire figure. This type of self-similarity at all scales is a hallmark of the images known as fractals.
Fractional Dimension
The word fractal actually comes from the notion of an object having a fractional dimension. In other words we can have an object existing in a dimension between the first and second dimension or the second and third dimension etc. A point has dimension 0, a line has dimension 1, and a plane has dimension 2. So how is it we can have something that has a dimension of 1.6 or 2.34? Again I found a wonderful link that explains it good enough that even I (an artist) can understand it.
http://math.bu.edu/DYSYS/chaos-game/node6.html
Understanding Marko’s piece
Midwinter night's dream (click here)
Marko’s piece has 6 triangular shaped words stacked together to form a larger triangle each of the words in this structure have white letters except one that shines yellow-orange. When you first click on this piece six words appear and if you notice the yellow-orange letters also spell a word. When I first started clicking on the words I could not make out any pattern. However, once I started writing them down I noticed that the triangular word that I clicked upon was soon duplicated throughout the entire structure of the large triangle with the yellow-orange letters. So in effect the smaller triangle conceptually contained the larger structure within its smaller structure. Thus being self-similar! A fractal made of words!
If you don’t get this at first then just think of each letter in the smaller triangle as being the possibility of also being the yellow-orange letter in a larger triangle and when you click on the small triangle it pops into a large triangle made of 6 more words. The larger triangle is contained in the smaller one you just can not see it because the resolution of the screen gets in the way … there are countless levels you can go through with this poem (its not really countless there is a finite number) but the bottom being it is a very beautiful structure.
I asked Marko about his choices for the words in the piece and the following in blue is his response:
In the Midwinter piece, there's the "source text," consisting of all the six-letter words from "Midsummer Night's Dream" by Shakespeare, in their original order. When you click for instance the word "hermia," the program gathers all the words from the source text which include the first letter of the clicked word, in this case "h", the first letter of "hermia." Then the program chooses one of those words at random and, after that, the program chooses the next word after previously chosen word in the source, which includes the second letter of the clicked word, in this case "e", and so on, until six words are chosen. Those six words are then displayed on screen, and the letters "h", "e", "r", "m", "i", and "a" are higlighted. This process takes place again and again, after each clicking.
So my next thought what is the fractional dimension for Marko’s piece? Here is the link again to help you:
http://math.bu.edu/DYSYS/chaos-game/node6.html
Here is our equation:
My mother sent this to me:
It is currious to note that on Wednesday of this week, at two minutes and three seconds after 1:00in the morning, the time and date will be
01:02:03 04/05/06.
This won't ever happen again
You may now return to your normal stuff
I received an interesting email from Finland yesterday. A mathematical poet there named Marko Niemi sent me some links to some mathematical vispo. One link in particular, directed me to one of his interactive math poems. I have to declare this is my favorite mathematical vispo piece to this date. It is a fractal poem and due to the fact, I have never seen one before, I find it quite exciting. Before I go into the details of how it works, I am going to leave it with you to figure out. I had a lot of fun poking around to see how it works and when the fractal element hit me, I was quite surprised. Marko’s hint was to click on one of the words to “zoom in”
Midwinter night's dream (click here)
I will be discussing the details in a future blog entry.
I wanted to share something that Scott Glassman wrote to me, which I find elegantly written. However, I don't want to appear pretentious and hope no one feels that my blog has advanced mathematics … all of what you find here, at this time, comes from the first and second semesters of algebra based physics. I am primarily an artist not a mathematician.
If there's anything verbogeometric / mathematical poetry can accomplish, at the very least, it can begin to help people understand that human qualities, spiritual qualities, operate in many dimensions-- they are the true conceptual equivalents (& metaphorical equivalents) of physical wonders, like say neutrinos. I see how the incorporation of these concepts with advanced mathematics begins to illustrate a depth and a myriad of functional "flourishes" (as say, experiences with music) that is closer to the truth. It begins to get at that "one hidden stuff" of which we are all made.
Scott Glassman
http://scottglassman.blogspot.com/
Thank you Scott for your kind words,
Kaz
I was attending an opening for the Imperial Beach Art Guild show held March 4 in Imperial Beach, California and happened to run across an artist there who was wearing a t-shirt that said, “5 out of 4 people have a problem with fractions.
Lets look at it in equation form:
I find it to be a nice math poem with a very curious metaphoric image in it. Five fourths of the population is a party balloon slightly twisting your mind before it blows up in your face. This twist of denotation turning into connotation sets up great tension, then exploding into a joke, as you walk away … some of us savor this kind of nonsense.
2.7. Distance Formula and Verbogeometry. As we have seen, to calculate the distance between two points, we need to describe our points by its coordinates using the nomenclature of the coordinate pair. Let me reiterate, describing a point in verbogeometry is no different from numerical coordinates except we use words. Lets look again at the example in figure 15 where we used the midpoint formula to find the exact point between the points: P1(love,praise) and P2(hate,punishment) but instead of putting them in the midpoint formula lets put them in the distance formula. (See figure 32)
Figure 32
Here we have an expression for the distance between the points P1(love,praise) and P2(hate,punishment) in two dimensions. But we can also use verbogeometry in any number of dimensions including hyper-dimensions. But before we look at hyper dimensional verbogeometry lets look at another example which we will express in the third dimension. The following example uses a three dimensional Cartesian coordinates system with 3 simple antonym word-axes. (See figure 33) The first axis is noble / ignoble the second axis is just / unjust and the third axis is loyal / disloyal.
Figure 33
Now lets look at the expression for the distance between the points P1(noble,just,loyal) and P2(ignoble,unjust,disloyal) see figure 34
Figure 34
Notice the green line in figure 33 is the visual representation for the mathematical expression above. However, it would be much easier to visualize if we were able to rotate the axis. Figure 33 is an isometric view, which I chose to use because it is best for viewing the axis but unfortunately at the expense of viewing the spatial orientation of the green line.Now let us look at verbogeometry in a hyper-dimension. Let us look at the distance formula used in seven dimensions:Figure 35 shows the mathematical poem 1+1+1+1+1+1+1+1 =1 This is a metaphorical piece that creates a metaphoric path from the concept of confusion, to where seven deities meet. The piece uses the analytic geometry distance formula in a seven dimensional space where each dimension is a gradation from confusion to a point where a deity exists.
2.6. The Distance Formula and Pythagorean Theorem: The distance formula uses the Pythagorean Theorem to calculate distances on the Cartesian coordinate system. The Pythagorean Theorem says that the hypotenuse of a right triangle is equal to the square of it sides. (see figure 26)
Figure. 26
solve for c and we get the following see figure 27
Figure. 27
Let us plot two points on a two-dimensional axis system P1(-9,10) and P2(4,3) and If we draw a lines between the points and lines parallel to the axes we can obtain a right triangle. (see figure 28)
Figure. 28
To solve the length of the hypotenuse we first find the difference between the x values and the y values to create the sides of the triangle then we plug the values into the Pythagorean Theorem.
x value is 9 - 4 = 5 and the y value is 10 - 3 = 7
Now we plug it to the equation and we get the expression in figure 29
Figure 29
The distance or length of the hypotenuse would be the square root of 74 or approximately 8.602
The distance formula is thus:
Given two points (x1,y1) and (x2,y2) (see figure 30)
Figure 30
Now what we have been looking at up till now has been in two-dimensions but we can also express a distance in many dimensions. Let us look at two points in three dimensions.
P1(x1,y1,z1) P2(x2,y2,z2)
If we were to put these two points into the distance formula it would look like what is shown in figure 31
Figure 31
It is evident that we can use the distance formula in uncountable dimensions all we have to is to add another dimensional term to the formula for every dimension we wish to express.
2.5. Prismatic Structures in Verbogeometry: Notice that 'barren and infertile' is a complex antonym and 'fertile and infertile' is a simple antonym as previously defined. This is interesting because we can see that there exists in verbogeometry a geometric construction where a line expressed as a simple antonym is normal (90 degrees) to a plane containing all of the complex antonyms related to the line which is expressing the simple antonym. To illustrate this idea lets look again at the relationship between the simple antonyms 'fertile' and 'infertile' and the synonyms 'barren', 'fruitless', 'unproductive', 'sterile', 'impotent' which reside on the plane that is normal (90 degrees) to the line created by the simple antonyms. Furthermore you can draw lines from all of the synonyms back to the complex antonym 'fertile'. (See figure 19)
Figure 19.
This idea also lends itself to prismatic structures where we have a group of parallel simple antonyms whose endpoints construct polygonal faces on two parallel synonym-planes. (See figure 19) Example: Let us define one synonym plane containing the words 'pleased', 'content', 'affected', 'satisfied', 'enchanted' and 'sympathetic'. The other plane contains the following simple antonyms for the previous group of synonyms: 'displeased', 'discontent', 'disaffected', 'dissatisfied', 'disenchanted' and 'unsympathetic'. Due to the synonyms of one plane have corresponding simple antonyms which create lines 90 degrees from the synonym-plane then the simple antonyms are synonyms of each other and reside on their own individual synonym plane and because the lines are 90 degrees to each other the planes must be parallel. The former verbiage is a lot easier to understand visually (See figure 20)
Figure 20.
On a side note: Everything that we have been talking about up to this point has been viewed in Euclidian space. Not much time has been spent exploring verbogeometry outside of Euclidian space. However, I see that there can be a lot more thought evolving models of verbogeometry in other spaces. For example, Instead of viewing antonyms and all the varying meanings spread out across a number-line, we may think of the antonyms as magnetic dipoles. Furthermore, all the varying meaning between them is analogous to a magnetic flux. Yet again, another view may be looking at the antonyms residing at the endpoints of a major axis of a three dimensional ellipsoid and the varying meanings reside on the surface of the ellipsoid. (See figure 21)
Figure 21.
Figure 22 shows an ellipsoidal flux-like paradigm for the previous prismatic structure. (See figure 20)
Figure 22.
Figure23 shows an unlabeled side view
Figure 23.
It may be easier to see the ellipse structure if it was wireframe (See figure 24)
Figure 24.
Figure 25 shows 5 parallel word axes in a wireframe structure
Figure 25.
2.4. Verbogeometry with Trigonometry: First let us solve a pertinent traditional trigonometric problem, which requires a solution for an angle. Let us make 'theta' the variable of the angle in question. The tangent of a right triangle is defined as the ratio of the side opposite the angle 'theta' to the side adjacent to the angle 'theta'. If we call the side opposite distance "y" and the side adjacent as distance "x" we then arrive at tan (angle theta) = y/x (See figure 16)
Figure 16.
It also follows that if we know the distance of two sides of a right triangle we can find all the angles. Let us look at an example with the side opposite angle theta being 3 and the side adjacent to angle theta being 4 and. Let us now solve for the angle theta. We know that y/x = tan (theta) so it follows ¾ = tan (theta). To uncover the value of theta, we must take the inverse tangent of ¾. Symbolically this is stated as "theta = inverse tan(y/x)" or approximately 36.87 degrees (See figure 17).
Figure 17.
In general, to reveal the angle after you have calculated the value for the tangent of y/x, your choice is to find the angle on a trigonometric table (old method) or you plug the values in on a hand held calculator.
Now let us look at a similar expression using verbogeometry and looking for the value of angle theta. This time we define the y distance as the difference between the concepts of barren and infertile (think number-line again) and let us define the x distance as the difference between the concepts of infertile and fertile. (See figure 18)
Figure 18.
If we want to know the angle of theta we have to take the inverse tangent of y/x or the inverse tangent of (barren - infertile)/(fertile - infertile) (see figure 18)
2.3. Midpoint Formula in Verbogeometry: Any analytic geometry equation can use coordinate word-pairs instead of numbers to express poetic forms. Let us use the midpoint formula to express the exact point between the two points P1(praise,love) and P2(punishment,hate) from figure 13. Before we look at coordinate word-pairs let us refresh the use of the midpoint formula in analytic geometry. To find the midpoint between two points on a Cartesian coordinate system we add the x coordinates together and divide by 2 to find the x value for the midpoint and we also add the y coordinates together and divide by 2 to find the y value for the midpoint or
(x1 + x2)/2 = x0 and (y1 + y2)/2 = y0.
Lets look at an example of finding the midpoint P0 between the points P1(-14-15) and P2(12,11) utilizing the midpoint formula. x1 = -14 and x2 = 12 so substituting our numbers in the variables of the equation (x1 + x2)/2 = x0 we get (-14 + 12)/2 = -1 also y1 = -15 and y2 = 11 so substituting our numbers in the variables of the equation (y1 + y2)/2 = y0 we get (-15 + 11)/2 = -2 therefore: P0 = (-1,-2) (see figure 14.)
Figure 14.
Let us now take a different approach and replace the numeric variables in the midpoint equation with the words/concepts of love, hate, praise and punishment. We will use the form of coordinate word-pairs P2(love, praise) and P1(hate, punishment). The midpoint formula now shows us that P0(x0, y0) will be formed by the substitution of (x1 + x2)/2 = x0 with (love + hate) = x0 and (y1 + y2)/2 = y0 with (hate + punishment) = y0. Now we have expressed the exact point between love, praise and hate, punishment. (see figure 15.)
Here is a relative piece from 2000 http://www.kazmaslanka.com/midpoint.html
2.2. Word-coordinate Pairs: We have witnessed a word-axis with different values of an antonym pair along a particular axis 'x' or 'y' in one dimension. (See figure 3) We also have seen a word-plane with values of two antonym pairs along two axes 'x' and 'y' in two dimensions. (See figure 10) Furthermore, we can have word-cubes along the x, y, and z-axes in the third and word-hypercubes in the fourth dimension or we can have antonymic pairs in innumerable dimensions. There is no limit to the dimensional palette for our expressions. Each antonym word-pair adds a new spatial dimension to our expressive construction. Let us talk about the spatial accuracy in defining the location of words in space. Once again, let us look at figure 10 and notice the antonym word pairs, just/unjust and noble/ignoble. However, let us focus our attention to the word-axis just/unjust. We know that we have defined a one-dimensional word-axis with different values of just and unjust but we do not know exactly where each of the words is located along the axis. We have no quantitative value for just or unjust. However, we do have a qualitative value and we know that the word exists somewhere on the axis. What is most important to us in verbogeometry is not the value as such, but the spatial relationship of the values to each other in space. Because the value or the meaning of a word is relative to the context in which it is used, each viewer individually creates his or her own context for meaning. Therefore, exact quantification of the word or its location in space is not possible. However, in some cases, it may be possible to restrict the context to a level where repeatable correlations exist, but those studies are more akin to denotation for the purpose of science. Scientific experimentation "proves" the equation to be mathematically correct and workable within a range of acceptability. In other words, experimental data defines viability of the relationships between the concepts in a scientific equation. On a side note: (When scientific equations are in the intuitive stages of development, there may be an argument to claim that they are in the realm of art, I personally might accept this view if it were not for the fact that their intention is not to make art.) In verbogeometry, we construct equations based on relationships between the qualities of our experiences to evoke meaningful aesthetic expressions of which most are connotative but some may be denotative.Let us get back to the Cartesian coordinate system for a moment and reiterate the idea of coordinate pairs. A point on a two dimensional coordinate system would have values for x and y and would be expressed as such: (x,y) (see figure 1.) A point on a three-dimensional axis system would have values for x, y and z and would be expressed as (x,y,z). A four dimensional point would be expressed as (x,y,z,w) in the fifth dimension as (x,y,z,w,v) etc.Before we get into multidimensional word-axes let just look at a simple two-dimensional word-plane with two word-axes. (see figure 12.)
Figure 12
The vertical axis is a synonym word-pair of praise and punishment and the horizontal axis is a synonym word-pair of love and hate. It is very important to realize that not only does the words love and hate define the identity of the horizontal or x-axis they also hold conceptual points in space along the axis and the same for praise and punishment with respect to the y-axis. The words which are conceptual points in space define a metaphoric value along its respective axis and can be notated as a coordinate pair similar to (x,y) So you may ask what would a coordinate word-pair look like? Let us look at the two points identified as point 1 or P1(love,praise) and point 2 P2(hate,punishment) (see figure 13.)
Figure. 13
