Mobius Poem by Endwar

Here is a link to a wonderful Mobius Poem by Endwar. Very Nice!
Click here for the Mobius Poem

Prometheus Epistle to Job

Do the muses scatter ancient fragments of thought or do they just perpetuate them. How is it that the ancient Greek Titans can still speak?

also see Orthogonal Space Poem

The Virtuous Sphere (part two)

The Virtuous Sphere (part two)
This blog entry is a continuation of “The Virtuous Sphere” please read the last blog entry so that today’s will make sense.

On the last blog entry, we had just finished talking about the equation of a sphere. However, the next question one may ask is, “why are there words in the equations instead of numbers?” To answer this question, you should read my essay on verbogeometry. I am going to republish some of the essay that relates to “The Virtuous Sphere” but if you have not read the essay on verbogeometry then you may not get as much out of this as you would if you were to read it.

Distance Formula and Verbogeometry: As we have seen, to calculate the distance between two points, we need to describe our points by its coordinates using the nomenclature of the coordinate pair. Let me reiterate, describing a point in verbogeometry is no different from numerical coordinates except we use words. Lets look again at the example in figure 15 where we used the midpoint formula to find the exact point between the points: P1(love,praise) and P2(hate,punishment) but instead of putting them in the midpoint formula lets put them in the distance formula. (See below)

Here we have an expression for the distance between the points P1(love,praise) and P2(hate,punishment) in two dimensions. But we can also use verbogeometry in any number of dimensions including hyper-dimensions. But before we look at hyper dimensional verbogeometry lets look at another example which we will express in the third dimension. The following example uses a three dimensional Cartesian coordinates system with 3 simple antonym word-axes. (See below) The first axis is noble / ignoble the second axis is just / unjust and the third axis is loyal / disloyal.
Now lets look at the expression for the distance between the points P1(noble,just,loyal) and P2(ignoble,unjust,disloyal) (see below)
Notice the green line in figure 33 is the visual representation for the mathematical expression above. However, it would be much easier to visualize if we were able to rotate the axis. Figure 33 is an isometric view, which I chose to use because it is best for viewing the axis but unfortunately at the expense of viewing the spatial orientation of the green line.

(The virtuous sphere is written in the language of three dimensions. What I find interesting is that we can write a spherical equation in hyper dimensions. The following shows the distance formula written in a hyperdimension.)

Now let us look at verbogeometry in a hyper-dimension. Let us look at the distance formula used in seven dimensions:Figure 35 shows the mathematical poem 1+1+1+1+1+1+1+1 =1 This is a metaphorical piece that creates a metaphoric path from the concept of confusion, to where seven deities meet. The piece uses the analytic geometry distance formula in a seven dimensional space where each dimension is a gradation from confusion to a point where a deity exists.

Here is a detail:

Lets look at the coordinate pairs for these two points P1(confusion, confusion, confusion, confusion, confusion, confusion, confusion) and P2(Allah,Buddha,Jesus,Spider woman,Vishnu,Yahweh,Zeus)

The Virtuous Sphere (part one)

The Virtuous Sphere (part one)

I thought it would be a nice idea to post "The Virtuous Sphere" and talk some about it. First of all I would like to say that I believe there are many ways to define virtue, this is only an artist rendition of one way. Please do not get bound up here in the idea of some absolute truth… remember the Hindu saying: “All wars are Just on both sides” When this piece was originally mediated to me my intentions were not so much interested in an answer of denotation but in the aesthetic inherit with the structure of a mathematical sphere and the coloration and distortion of that sphere by the personal ideas of integrity, justice, nobility and of course virtue.

Today's blog entry will talk about the analytic geometry involved in the piece and the next blog entry will discuss the verbogeometrical ideas needed to approach this piece.

Let me talk a little about the mechanics of this piece. This piece is a standard verbogeometry piece so obviously I will be borrowing sections from my essay on verbogeometry to help open this up for you that are not familiar.

We all should be able to recognize a sphere, but did you know that a sphere has a relationship to the Pythagorean Theorem? To see this relationship we first should talk about the relationship between the distance formula and the Pythagorean Theorem. Then we will look at the relationship between the distance formula and a circle and after that the sphere. The distance formula uses the Pythagorean Theorem to calculate distances on the Cartesian coordinate system. The Pythagorean Theorem says that the square of the hypotenuse of a right triangle is equal to the sum of the square of it sides.

Solve for c and we get the following:


Let us look at little closer at how the Pythagorean Theorem works in a Cartesian coordinate system. Here is an example: Plot two points on a two-dimensional axis system P1(-9,10) and P2(4,3) and If we draw a lines between the points and lines parallel to the axes we can obtain a right triangle.

To solve the length of the hypotenuse we first find the difference between the x values and the y values to create the sides of the triangle then we plug the values into the Pythagorean Theorem. The x value is 9 - 4 = 5 and the y value is 10 - 3 = 7Now we plug it to the equation and we get the expression in the following figure:

The distance or length of the hypotenuse would be the square root of 74 or approximately 8.602

The distance formula in two dimensions is thus -- Given two points (x1,y1) and (x2,y2):

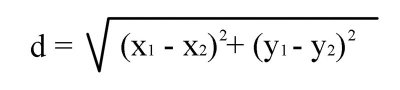To reiterate -- you will notice that the distance formula is nothing more than Pythagorean Theorem placed on a Cartesian coordinate system! The x1-x2 in our equation actually shifts the line horizontally and the y1-y2 shifts the line vertically. In effect if we start at the origin for our point (x1,y1) then we can simplify the equation as shown below:

Let us look at the equation for a circle: (below) --- Doesn’t it also look remarkably like the Pythagorean Theorem? In essence it is the Pythagorean Theorem! Notice that the radius of the circle corresponds to the hypotenuse of the right triangle. What we do is sort of ‘nail down’ one end of our right triangle at the hypotenuse and spin it around so that the other end of the hypotenuse follows the form of a circle.
All of the equations that we have been looking so far function in two dimensions but what if we wanted to use the Pythagorean Theorem in three dimensions? To use the Pythagorean Theorem or the distance formula in three dimensions we append another term at the end of the equation so it looks like the one below.

The Pythagorean Theorem in three dimensions is the same as it was in two dimensions except that we add another term at the end to give us the extra dimension.

Let us look at the equation for a sphere (below):

Notice that it looks just like the Pythagorean Theorem in three dimensions? It follows the same thought that we did in two dimensions. Where we ‘nail down’ one end of the triangle and spin it around in a circle but since we are in three dimensions, we also spin the circle around an axis and so it goes that the end of the triangle we started with now follows the form of a sphere.

This concludes discussing the analytic geometrical aspects of “The Virtuous Sphere” You can see that I used the equation for a sphere as my mathematical language for this piece. The only thing we haven’t discussed is the verbogeometric properties of the piece. The next entry in my blog will discuss some of the mechanics of verbogeometry that are needed to approach this piece.

A Screening of Super-8 films by Robert C. Morgan

I studied with Robert C. Morgan in the late 1970’s and he is responsible for much of my earlier artistic development. He exposed me to the conceptual art movement in general and Benar Venet in particular. Venet noticed that science had aesthetics as well as art and was bold enough to re-contextualize these scientific aesthetics as Art. It wasn’t until I read the Dancing Wu Li Masters by Gary Zukav that I experienced an epiphany that drove me into mathematics and science. Prior to that event I had no interest in mathematics and some disdain. However, I must say I loved math up until I was seven years old then, as I mentioned, I abandoned it until 1979.
Robert has always been supportive and I always wish the best for him.

Millennium Film Workshop

presents


A Screening of Super-8 films by Robert C. Morgan

Saturday, June 17, 2006, at 8 PM



Although known today primarily as a critic and curator, Robert Morgan
emerged as a "post-conceptual" artist in the mid-seventies. Between 1974 -1989,
Morgan worked in a variety of different media, including an extensive body
of work in Super-8 film. He regards his films as "counter-narrative" in that
they deconstruct both Hollywood and commercial television -- the two primary
forms of visual narrative in the entertainment industry -- by laminating appropriated
footage against a personal and often political narrative. This is a rare opportunity
to see films by one of the formative "appropriation" artists of the seventies.

A reception will precede the screening in the Millennium Gallery at 7 PM

Admission: $8 / $6 (members)


For further information, please contact:

Millennium Film Workshop
66 East 4th Street, NYC 10003
Tel & Fax: (212) 673 - 0090
Email: cinema@millenniumfilm.org

The Transformation of Poison

The image above has been simmering in the background for a few years now and has finally come to fruition. It came about in December 2001 over a cup of coffee while taking a break at the ASCI conference in NYC. At the conference I met a very interesting Poet/Artist Philosopher and NASA scientist named Farzad Mahootian. We had a wonderful conversation between sips of dark java in mid town Manhattan and talked of many things. I shared my ideas on verbogeometry while he shared his ideas on sculptures that purify the environment. In our mutual excitement he thought it would be a good idea to incorporate the two ideas into a piece of Art. The piece above is the result. I decided to make a symbolic wedge from a verbogeometric prism and have it cleaning the air with chrysanthemum power.

Terminology for Mathematical Poetry and Related Endeavors*

‘ Visual Art Aesthetic’ is the aesthetic that concerns itself primarily with the beauty or horror expressed in direct sensory experience, whereas the ‘ Mathematics Aesthetic’ concerns itself with the beauty in the structures of logic and thinking.

‘Mathematic Aesthetic’ is the aesthetic that concerns itself with the beauty in the structures of logic and thinking, whereas the ‘Artistic aesthetic’ is concerned primarily with the beauty expressed in direct sensory experience.

'Mathematical Conceptual Art’ This form of Art focuses on the Math aesthetic and re-contextualizes it as Art personally I feel conceptual art is not art however, it is aesthetic but. That does not necessarily mean that Math is art. The main difference between ‘Mathematical Conceptual Art’ and ‘Visual Mathematics’ is that in the former the artist presents their the work as Math, where as in the later they display the mathematical object as Art. In both types, they display the object in the context of an Artistic space. A good example of “Mathematical Conceptual Art’ would be the work in the late 1960’s of Benar Venet in which he would study Math and Physics and present what he had learned purely for the aesthetic of the topic involved. There are many works of Sol Lewitt that could be considered “Mathematical Conceptual Art’ as well. A contemporary Artist who I would consider a ‘Mathematical Conceptual Artist’ is the British artist Justin Mullins although he does some work that could be considered as ‘Mathematical Visual Poetry’. The main difference between Mathematical Conceptual Art and Mathematical Poetry is that the Conceptual Art movement as a whole was not concerned with the intention of metaphor in any form and Mathematical Poetry relies mostly on metaphor to make its connection to poetry in general

‘Mathematic Constructivism’ Is one of the most popular forms of Mathematically related Art. It is a term I will use to sum up a conceptual thread that started with the Russian constructivists and ended up in the modern movement of visual mathematics. The former started in the political and social upheaval of the 1920’s with the emergence of Artists such as Naum Gabo, Vladimir Tatlin and ended up in the latter movement with mathematicians such as Donald Coxeter who felt their mathematical work is a form of Art. Donald Coxeter imparted much mathematical assistance to M C Escher.
The conceptual idea of Cubism pushed visual Art into a process of abstraction whereby the artist removes unnecessary visual layers of an object in order to point to a metaphysical idea of the object. Art Constructivism moved to push the methodology of abstract Art more and more abstract to the point of the object being something not found in nature -- a “construction”. If we push this idea further we end up in realm of ‘Visual Mathematics’ where the object of Art is pure logic, a reflection of the logical structures of language in our mind. Today ‘Mathematical Constructivist’ work has moved more toward ‘Visual Mathematics’ and can be seen in the work of Max Bill, Helaman Ferguson, Rinus Roelofs, Robert Fathauer, Brent Collins and many others.

‘Mathematical Poetry’ – Mathematical Poetry is a umbrella term that covers any poetic expression involving Mathematics. An initial list of categories is as follows: Equational Poetry, Mathematical Visual Poetry, Visual Mathematical Poetry, Mathematics Poetry and Number Poetry


‘Equational Poetry’ – This is literally performing mathematical operations on concepts whether they are words or images. A good example would be my page at the following link: Mathematical Poetry

'Visual Mathematical Poetry' -- This is a mathematical poem where the elements in that poem are visual objects. The difference between mathematical poetry and visual mathematical poetry is that the former uses words and the later uses images. Visual mathematical poetry is more similar to mathematical poetry than it is to mathematical visual poetry. However, one could create a poem that has aspects of all three of these types. For an example check out "Americana Mathematics"
‘Mathematical Visual Poetry’ – This is more difficult to define because of the vast areas and the many competing definitions of visual poetry. However, I consider mathematical operations on text as well as mathematical textual information composed for aesthetic purposes to be ‘Mathematical Visual Poetry’ Also words, text or textual elements mixed with mathematical symbols or formulae that are not performing mathematical operations on the word meanings. Although Karl Kempton has worked in many categories, I feel the following is a good example of ‘Mathematical visual poetry’: Another good example is Marko Niemi’s fractal poem described in the following link: Midwinter nights dream Scott Helmes was one of the first visual poets that moved into mathematical motifs. Bob Gruman has probably been the most prolific in this catagory.

‘Mathematics Poetry’ -- This poetry is what I would call traditional language poetry about or inspired by or uses mathematical imagery. I also would consider this catagory to include language poetry that has an interaction of numbers with words. There are numerous examples all over the web but the most popular from google's perspective seems to be Marion Cohen: other sources would be JoAnne Growney and Katherine Stange:

'Polyaesthetics' is a word used in relation to aesthetic works which incorporate many diverse aesthetics. This is not limited to but includes the aesthetics of Mathematics, Art, Music, Science, Religion etc.

'Visual Mathematics' Is one of the most popular forms of mathematically related art. It sometimes has been called “Concrete Art” This is a form of Art that focuses on the Math aesthetic and re-contextualizes it as Art. The main difference between ‘Mathematical Conceptual Art’ and ‘Visual Mathematics’ is that in the former the artist presents his/her personal/emotional relationship with the aesthetic of Mathematics where as in the later the display is less personal and more cerebral. In both types the object of that presentation is displayed as a form of Art. The hero of visual mathematics is M C Escher whose work is so strong anything that resembles it looks cliché. Fortunately there are other arenas in Visual mathematics. A good example of contemporary Visual Mathematics is found in the work of George Hart, Paul Gailiunas, Carlo Sequin, Robert Krawczyk, Michael Sussna and many others. This type of work is primary interested in visualizing mathematic structures. These structures could be anything from computer algorithms not limited to fractal Art or polytopes to hand drawings, plastic sculpture or origami.


*Disclaimer: These are the views of Kaz Maslanka and are a rough attempt at trying to put mathematical poetry in context with most of the mathematical influences in visual Art of the last 100 years

Polyaesthetic example

Boeing 747 Landing gear in the process of being manufactured

Walt Gillette of Everett, the lead engineer on the 787 program and a man Business Week recently called a "plane genius," announced his retirement from the Boeing Co. on Wednesday.

You may ask what does this event have to do with mathematical poetry? … Not much however, the following quote of his is a perfect example of polyaesthetics whereby aesthetics comes in many forms even in engineering and technology.

Walt Gillette says,
"One of the most incredible experiences is to go out ... and stand in the middle of full landing gear of a Boeing 747," he said. "To stand there, right there under that big, fat, huge machine, and you think this thing goes 625 miles an hour and a little-bitty human brain ... tells it exactly what to do and where to go, and it follows just like a docile family pet."

There are many forms of beauty in concepts and some say that if the concept is beautiful then it must be considered as a form of Art. I personally don’t find beauty and Art to be synonymous but I will admit that it is a nebulous concept and very difficult to nail down. Art for some reason seems to be a ‘catch all’ for anything anyone wants to call Art. I wish there was a better ‘catch all’ term other than Art. If you can think of one then I invite you to comment.

More Math Humor

click on it to read

It seems I have found myself in a sexist corner again … I was feeling a bit guilty for posting "girls = evil" so I had to post the cartoon above to give equal voice to our lady friends.

smile! its not that bad :)

Fabulous Finnish Fractal Flooring

Nokturno.org has a new fractal poem titled Palasista!
by Saara Lehto. The piece is written in Finnish and is in the form of a Sierpinski Carpet. The words are all anagrams of each other as well as the title.

Thanks to Marko Niemi for bringing this to us!

Rescuing Metaphor

Gregory Vincent St. Thomasino has sent me a math poem that I would like to share with you.

to + to = too

This is a nice little poem that has three Important elements that strike me right off the bat:
1.) it plays on the words to and too … in other words we have too many to's
2.) is the clever addition of o's … o + o = oo
3.) the most important element of any mathematical poem is the equal sign.**

I really like the feeling in this piece … metaphor is so hard to describe without using another metaphor and if we do then we miss the point.

By the way … eratio seven is now available! Check it out!


** It is the equal sign that creates the metaphor in mathematical poetry. It is the fact that a poem of the latter form says a + b = c and we know that a + b IS NOT c

There exists a mathematical form that is the logical crux of all metaphors in all poetry mathematical or otherwise:
A = B
Given: We know for a fact that ‘A’ does not equal ‘B’

There is also one more key ingredient for metaphor to exist. That ingredient is connotative intention. In other words, the physics equation d = vt is not metaphorical because the intention of the equation is denotative.

‘A’ is similar to ‘B’ is not a metaphor
‘A’ is proportional to ‘B’ is not a metaphor
‘A’ looks like ‘B’ is not a metaphor
‘A’ is compared to ‘B’ is not a metaphor
Simile is not metaphor that is why they are different words

Marius de Zayas

Marius de Zayas and Francis Picabia, FEMME!

Karl Kempton shares some links with us:

Marius de Zayas, Agnes Meyer. Eye Contact: Modern American Portrait Drawings from the National Gallery, Nov 2005

Picabia. Between Music and the Machine: Francis Picabia and the End of Abstraction, fig 28 mathematical formulas. Nov 2005.



I really am not able to tell whether Zayas was trying to express something mathematically or not. I have seen an abundance of artists decorating their work with equations in order to express a math feeling or maybe add a cryptic quality to their works and that may be what Zayas is trying to do as well …These days the latter idea is a bit trivial however, the case with Zayas is probably one of the first times that equations are inscribed within visual work … (I wouldn’t put it past Hieronymus Bosch … but I don’t think he did it)

Thanks Karl for passing this on!

Three Different Kinds Of Mathematical Poetry

There are many who claim the endeavor of ‘mathematical poetry’ and we can see as many forms as there are claims. I personally see three different forms however, the second category I describe may be broke into many other forms. I will list them in order of popularity at this time in 2006. I also want to mention that I am not one to engage in taxonomy for taxonomy’s sake but delineate things only if I feel there is confusion. There also can be works that incorporate all three categories.

1. ‘Mathematics poetry’ -- This poetry is traditional language poetry about or inspired by mathematics. I also would consider poetry that plays with numbers and words in this category. There are numerous examples all over the web but the most popular from my perspective is Marion Cohen:
Another source would be Katherine Stange:
2. ‘Mathematical Visual Poetry’ – This is more difficult to define because of the vast areas and the many competing definitions of visual poetry. However, I consider mathematical operations on text as well as mathematical textual information composed for aesthetic purposes to be ‘Mathematical Visual Poetry’ Also words, text or textual elements mixed with mathematical symbols or formulae that are not performing mathematical operations on the words. Although Karl Kempton has worked in all three categories, I feel the following is a good example of ‘Mathematical visual poetry’: Another good example is Marko Niemi’s fractal poem described in the following link: Midwinter nights dream
3. ‘Mathematical Poetry’ – This is literally performing mathematical operations on concepts whether they are words or images. A good example would be my page at the following link: Mathematical Poetry
Also the following link has an example of Scott Helmes: And Bob Grumman at the following link is a good example of a mixture of ‘Mathematical Poetry and Mathematical Visual Poetry’:

The mathematical poetry blog links page for Marko Niemi

Marko Niemi's Mathematical Visual Poetry:

Midwinter nights dream
http://www.nokturno.org/marko/haynaku/midwinter.html


The link above is my personal favorite of his and you can read my little essay about it click here

Fibonacci visual poem
http://www.nokturno.org/marko/nurotus/fibonacci/

The following is a Finnish visual poem based on the Sierpinski triangle

Kolmioita
http://www.nokturno.org/marko/nurotus/kolmioita/kolmioita.gif

Brownian motion series
http://www.nokturno.org/marko/brown/

"Eloquent Fern"
http://www.nokturno.org/marko/fern.html

The following statement is Marko's preface for the "Eloquent Fern"

The "text" in this piece is the following paragraph from "Rhetoric" by Aristotle, "translated" into four-letter DNA code: (It is clear, then, that rhetoric is not bound up with a single definite class of subjects, but is as universal as dialectic; it is clear, also, that it is useful. It is clear, further, that its function is not simply to succeed in persuading, but rather to discover the means of coming as near such success as the circumstances of each particular case allow. In this it resembles all other arts.)

Narcissus The series consists of six pieces, and in each piece, locations of individual letters are defined by the same polar coordinate function:RADIUS = A * cos(0.5 * ANGLE), where A is constant, and ANGLE goes from 0 to 720.The direction of each letter is independent from its location, but it's a function of ANGLE, too. This direction function is different in each piece, and it's the reason why pieces differ from each other, even though they all use the same location function.

Animated mathematical/scientific visual poems:
Critical Mass
Divine Intervention
Eye of the beholder
Party NRJ

New Mexico State University has acquired "Golden Fear"

GOLDEN FEAR
by KAZ MASLANKA

I am pleased and grateful to announce that the “University Art Gallery” at New Mexico State University has acquired a limited Edition Lambda Duratran of “Golden Fear” for their permanent collection.

Blends & Bridges: A Survey of International Contemporary Visual Poetry & Related Art

I feel grateful to be a part of the vispo show in Cleveland Ohio this month the show is full of a lot of very talented artists. Check out the link below.

VISPO!

Blends & Bridges: A Survey of International Contemporary Visual Poetry & Related Art

Gallery 324 at the Galleria at Erieview is hosting a show of contemporary international visual poetry (Vispo for short).

The show is curated by Cleveland visual poet/publisher John Byrum, Florida visual poet/publisher Bob Grumman, and Cleveland artist Wendy Collin Sorin.

Gallery 324
1301 East Ninth Street
Cleveland, OH 44114

click here for show index

Fractal Vispo by Marko Niemi

Fractal Visual Poetry

I want to get back to the fractal poem that was created by Marko Niemi and the post of mine from March 25th Midwinter night's dream (click here)

To understand some of the ideas incorporated into Marko’s piece we need to understand a little about this idea of fractals. Fractals have many facets of interest however; I want to focus on two:
1.) Self-similarity
2.) Fractional dimension

You may ask yourself, “Have I experienced a fractal in nature?” The answer is yes! I believe the easiest way to recognize that you have experienced one is by asking the question: “Have I ever noticed something that looks the same viewed at different scales: In another words the look very much the same whether I am close to it or far away.

Here is a short list of fractals patterns found in nature

*the branching of tracheal tubes
*the leaves in trees
*the veins in a hand
*galaxies
*water swirling and twisting out of a tap
*a puffy cumulus cloud
*tiny oxygen molecule, or the DNA molecule
*the stock market
*sea shells

I believe out of this list the easiest one to comprehend is a cumulus cloud. These kinds of clouds look the same from 60 feet away or 6 miles away. From either distance clouds basically have the same shape.
The picture below looks very much like the runoff from my neighbor’s water sprinkler before he got his Arizona lawn seeded properly.






But the fact is that I shot this photo of the Grand Canyon from one of my airplane flights between Denver and San Diego. Here we can see another self-similar example in the fact that water erosion looks pretty much the same from different scales.

Mathematical Fractals
We have all probably seen some ‘self similar’ mathematically created fractal images on the Internet or at a bookstore. However, to get a good understanding of it I wish to focus on the image below. The figure below is called a Sierpinski triangle named after the 20th century polish mathematician.
I don’t think that I could explain self-similarity any better than the following link so I stole the text “shown in red” from that site and posted it below:

http://math.bu.edu/DYSYS/chaos-game/node5.html

Self-similarity
One of the basic properties of fractal images is the notion of self-similarity. This idea is easy to explain using the Sierpinski triangle. Note that S may be decomposed into 3 congruent figures, each of which is exactly 1/2 the size of S! See Figure 7. That is to say, if we magnify any of the 3 pieces of S shown in Figure 7 by a factor of 2, we obtain an exact replica of S. That is, S consists of 3 self-similar copies of itself, each with magnification factor 2.

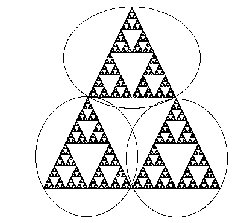
Figure 7: Magnifying the Sierpinski triangle

We can look deeper into S and see further copies of S. For the Sierpinski triangle also consists of 9 self-similar copies of itself, each with magnification factor 4. Or we can chop S into 27 self-similar pieces, each with magnification factor 8. In general, we may divide S into 3^n self-similar pieces, each of which is congruent, and each of which may be maginified by a factor of 2^n to yield the entire figure. This type of self-similarity at all scales is a hallmark of the images known as fractals.

Fractional Dimension

The word fractal actually comes from the notion of an object having a fractional dimension. In other words we can have an object existing in a dimension between the first and second dimension or the second and third dimension etc. A point has dimension 0, a line has dimension 1, and a plane has dimension 2. So how is it we can have something that has a dimension of 1.6 or 2.34? Again I found a wonderful link that explains it good enough that even I (an artist) can understand it.

http://math.bu.edu/DYSYS/chaos-game/node6.html

Understanding Marko’s piece

Midwinter night's dream (click here)

Marko’s piece has 6 triangular shaped words stacked together to form a larger triangle each of the words in this structure have white letters except one that shines yellow-orange. When you first click on this piece six words appear and if you notice the yellow-orange letters also spell a word. When I first started clicking on the words I could not make out any pattern. However, once I started writing them down I noticed that the triangular word that I clicked upon was soon duplicated throughout the entire structure of the large triangle with the yellow-orange letters. So in effect the smaller triangle conceptually contained the larger structure within its smaller structure. Thus being self-similar! A fractal made of words!

If you don’t get this at first then just think of each letter in the smaller triangle as being the possibility of also being the yellow-orange letter in a larger triangle and when you click on the small triangle it pops into a large triangle made of 6 more words. The larger triangle is contained in the smaller one you just can not see it because the resolution of the screen gets in the way … there are countless levels you can go through with this poem (its not really countless there is a finite number) but the bottom being it is a very beautiful structure.

I asked Marko about his choices for the words in the piece and the following in blue is his response:

In the Midwinter piece, there's the "source text," consisting of all the six-letter words from "Midsummer Night's Dream" by Shakespeare, in their original order. When you click for instance the word "hermia," the program gathers all the words from the source text which include the first letter of the clicked word, in this case "h", the first letter of "hermia." Then the program chooses one of those words at random and, after that, the program chooses the next word after previously chosen word in the source, which includes the second letter of the clicked word, in this case "e", and so on, until six words are chosen. Those six words are then displayed on screen, and the letters "h", "e", "r", "m", "i", and "a" are higlighted. This process takes place again and again, after each clicking.

So my next thought what is the fractional dimension for Marko’s piece? Here is the link again to help you:

http://math.bu.edu/DYSYS/chaos-game/node6.html

Here is our equation:

So Marko has 6 self similar pieces with a magnification factor of three. Therefore midwinter nights dream has a fractal/fractional dimension of approximately 1.63

Now isn’t that cool!

A numerically significant point in time?

My mother sent this to me:

It is currious to note that on Wednesday of this week, at two minutes and three seconds after 1:00in the morning, the time and date will be

01:02:03 04/05/06.

This won't ever happen again

You may now return to your normal stuff

Mathematical Poetry from Finland

I received an interesting email from Finland yesterday. A mathematical poet there named Marko Niemi sent me some links to some mathematical vispo. One link in particular, directed me to one of his interactive math poems. I have to declare this is my favorite mathematical vispo piece to this date. It is a fractal poem and due to the fact, I have never seen one before, I find it quite exciting. Before I go into the details of how it works, I am going to leave it with you to figure out. I had a lot of fun poking around to see how it works and when the fractal element hit me, I was quite surprised. Marko’s hint was to click on one of the words to “zoom in”

Midwinter night's dream (click here)

I will be discussing the details in a future blog entry.

Scott Glassman on Verbogeometry

I wanted to share something that Scott Glassman wrote to me, which I find elegantly written. However, I don't want to appear pretentious and hope no one feels that my blog has advanced mathematics … all of what you find here, at this time, comes from the first and second semesters of algebra based physics. I am primarily an artist not a mathematician.

If there's anything verbogeometric / mathematical poetry can accomplish, at the very least, it can begin to help people understand that human qualities, spiritual qualities, operate in many dimensions-- they are the true conceptual equivalents (& metaphorical equivalents) of physical wonders, like say neutrinos. I see how the incorporation of these concepts with advanced mathematics begins to illustrate a depth and a myriad of functional "flourishes" (as say, experiences with music) that is closer to the truth. It begins to get at that "one hidden stuff" of which we are all made.

Scott Glassman
http://scottglassman.blogspot.com/


Thank you Scott for your kind words,
Kaz