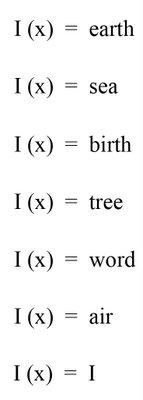The Energy To Break My Heart

Unfortunately to see it you must click here


This poem uses the physics equation for energy E = Fd Energy is also called work "W"

Energy (or work) is the force applied to an object multiplied by distance that object travels
If we pull force out of the context of the sentence above and look at what defines force we will find that Newton’s second law states Force is equal to the mass of an object multiplied by the acceleration the object is experiencing. Now if we look at acceleration we find that acceleration is the change in velocity per the change in time. In our energy equation we are multiplying the F times the distance the object is traveling. The way we calculate distances is with the distance formula. The poem above uses the distance formula in a nine dimensional space where every verbogeometrical axis is described in the poem underneath the radical.

Optical Illusion Contest

Here is something unrelated to mathematical poetry but interesting none the less. I received this information from my vision science list today. These are the results from the best optical illusion contest of 2006 --- If you are an interested vision scientist, they are now calling for submission to the 2007 contest.

Check out the winners of 2006 here
Go to this page then click on TOP 10 finalists

The History Of Numbers

Karl Kempton sent me this link ... all I could say was WOW!
check out all these books (click here)

Infinity In Science / Poetry

I tend to think that without logic, you cannot communicate and without communication, you cannot have a philosophy. To me logic presupposes philosophy ... Logic is the supportive structure for thought without it everything would fall apart, no one could predict where our next meal would come from, much less anything else. The other side of the coin is that without a philosophy coloring ones theory of logic, ones logic has no starting point. In this sense, ones logic can have no logic without a philosophical stone to stand on. It is a vicious circle!

The clipping below originally came from a polytope list and was sent to me by my friend the mathematician Paul Gailiunas. My original question to him a few weeks ago concerned the importance of infinity within modern scientific equations. Math poets seem to gravitate toward using infinity in our math poems and as professor Gailiunas told me scientists tend to avoid infinity as much as they can. The following is an example of scientific thinking in this area.

Kaz,
This came from a completely different direction.
I thought you might beinterested.
Paul

On Thu 7 Sep 2006 (21:46:48 +0100), guy@steelpillow.com wrote:On Wed, 6 Sep 2006 08:54:09, "Wenninger, Magnus" wrote:>the word Finitism caught my attention. Wow! I thought ...>This is something I have to bring to the attention>of our List. You can find it at:>http://plato.stanford.edu/entries/geometry-finitism/ In schools of divinity it is often said that philosophy is the handmaid of theology. But I think it is equally true that philosophy is the handmaid of>mathematics as well. How about that? At risk of wandering a little off the List's home territory, I find it hard to think of a discipline which does *not* rely on philosophy as its handmaid. Without philosophy there can be neither meaning nor logic, and without these there can be no rational thought or communication of ideas. I was of course intrigued to find another discipline where the broken natureof Euclidean lines causes a broken theory. I get the impression from Mathworld that discrete projective geometry is a fairly developed discipline, and I wonder whether finitists would, like us reciprocists (I shy away from"dualists" where theology appears in the same message!), do better to keep their distance from old Euclid's ghost. It seems to me that finitism is intimately bound to the philosophy of science. I recall the verification principle, favoured by logical positivists, that no statement has any meaning unless it can, at least in principle, be verified byexperiment. As a philosophical principle it fell at the first hurdle - how do we verify the verification principle itself? - and logical positivism soon faded from all but the history books. The principle remains a cornerstone of the scientific method - an article of faith that reality has an ultimate order. A finitist might observe that if something is suspected to be infinite, then this cannot be verified by experiment, and therefore no infinity has any scientific value. It follows that any mathematical model of any scientific phenomenon should preferably contain no infinities. Of course, if we seek a mathematical model of the underlying reality rather than the scientific observations alone, then we are using our maths to do philosophy and are not restricted to finitism.Modern quantum mechanics and general relativity are both plagued by infinities. Does this mean that they are in truth philosophical theories, with little to offer the hardworking scientist but approximations and embarrassing work arounds? If so, then where should philosophy end and theology begin? And why?

The Equation For Aesthetic Measure By Birkhoff

My friend Keith Rowley pointed me at the equation above by 19th century American Mathematician George David Birkhoff. The equation comes from Birkhoff’s 1933 book entitled “Aesthetic Measure”. Here is a perfect example of an equation intended for artistic purpose and yet denotative. Here Birkhoff intends to write an equation to measure levels of aesthetic based on a ratio of order and complexity. Personally, I feel trying to quantify something as broad as the word ‘aesthetic’ is extremely difficult and elusive. I have not read his book so I withhold more comment until I have read what he has to say. My intuition tells me what he is doing is much like my syncopation theory. It will be interesting to see what differences there are.

Scott Glassman Responds

Detail of Factorial for Scott Glassman (above)


Scott Glassman responds to my posting of his poem with my translations. I believe this gives even more detail to the workings of Scott’s poetry:

Kaz,

Your analysis is fantastic, and takes the poem to a very intricate term-bound level, one maybe lurking in logic + subsconscious forces. I always find the tension between emotions and quantification to be wonderful and you elucidate this beautifully in the visualized quotients.

I see how "I" an "I" is divided by elements, sun, burning, moon, etc. "I" or identity, or body, is a ratio of dust and cosmic energy, no better expressed than the direct equations you write out. Seems to cut through the bull to the crux of the matter.

The you - myself graphic you present is compelling because it made me think more about what I was, or my subconscious, was getting out. you - myself = luck. Or getting out of my own head, the ego, is a positive thing and will bring all the benefits. This is a frequent theme in what I write because I often try to disable the "I" and write from some central, unified place. luck = myself + you recognizes that in addition to self-disabling ego-dissolution work, there must also be an outside energy one connects with, an "other" on which "luck" is contingent. (Not really "luck" then anymore I guess is it). love is another product of myself + you.

myself + you = luck / love

an equal ratio of these elements, for someone in love is lucky and vice versa, seemingly to an equal degree

The final part you elucidate is probably the most fascinating because it appears at first to turn the whole logic on its head.

love = myself - you

What I think this is saying, or getting at, is the importance of letting go, of surrendering that which makes one most complete. That human beings or forces ALTHOUGH they may complement one another and co-exist in a single orbit, as do electrons of an atom-- one is not made subservient to the other, one is not made solely for the other's pleasure. Now I'm aware this is entering into the realm of the philosophical, the why-are-we-here-and-seperate question? And I suppose it speaks to the inherent integrity of nature, the particles that solid matter is made from, always particulate, having their boundaries as does the earth, moon, dewdrop, etc. Just above the unified plain, what is visible to the most powerful microscopes. Might be expressed:

myself - you = integrity / love

I'm linking the image and post to my blog. Thanks again for your attention to the poem, opening its dimensions for me.

Scott

Factorial By Scott Glassman

i
am a
quotient of the

sun
i am
a quotient of

the
moon i
am a quotient

of
the one
i am a

quotient
of the
two i am

a
quotient of
the burn i

am
a quotient
of the dew


2.

i
am a
multiple of the

earth
i am
a multiple of

the
sea i
am a multiple

of
the birth
i am a

multiple
of the
tree i am

a
multiple of
the word i

am
a multiple
of the air


3.

i
subtract myself
from you for

luck
i add
myself to you

for
love i
subtract myself from

you
for luck
i add myself

to
you for
love i subtract

myself
from you
for luck i

add
myself to
you for love


4.

i
am zero
over you +

1
i am
zero over you

+
2 minus
0 over you

+
1 minus
0 over you

plus
2 minus
you over me

+
0 minus
1 over you

The poem above is a poem by Scott Glassman called factorial taken from his blog.

I find this poem of Scott Glassman very interesting in that I can see it as an example of mathematical poetry buried inside mathematics poetry. (Click here for the difference between mathematical poetry, mathematics poetry and mathematical visual poetry) The first section of Scott’s poem I have transformed into a piece of mathematical visual poetry. (above) This mathematical visual poem shows four separate mathematical poems that are contained within section one of his mathematics poem.



The verses in the second section have different meanings dependent on whether the poem is lineated or written without lineation. However, both ideas are present in the poem. You can feel the tension between differing statements and the shift in context between the statements due to reading it lineated and then reading it not lineated. I have written out all the mathematical poems/verses I could find contained within this section and displayed them in the image shown above.



The third section functions much the same as the second as far as tension between lineation and reading it without the lineation. However this section has only two statements repeated three times. The interesting part in this section is that the lineation creates two more mathematical poems which are shown in black (above).



The fourth section is a bit more difficult to map out. Therefore I shot a photo of my deductions from the poem. (above) You can see the brackets point to three mathematical poems that are delineated by the brackets inside the mathematics poem. The third one of the three I used algebra to simplify the expression into a compact form/context. Watch the meaning change in this poem through all the metamorphoses.

Geof Huth Mathematical Poetry Links

This page is reserved for Geof Huth's Mathematical Poems and related material

Algebraic Poem #1

Algebraic Poem #2

Algebraic Poem #3

Algebraic Poem #4

Mathematical Graffiti

art@IIT Upcoming Show

Anonouncing the upcoming show art@IIT currated by my friend Robert Krawczyk

Introduction To ‘Visual Mathematical Poetry’

"Americana Mathematics" (above)

-Details Views (below)-

Introduction to ‘Visual Mathematical Poetry’:
I would like to introduce another category for mathematical poetry related nomenclature. This delineation I would like to call visual mathematical poetry. This is a mathematical poem where the elements in that poem are visual objects. The difference between mathematical poetry and visual mathematical poetry is that the former uses words and the later uses images. Visual mathematical poetry is more similar to mathematical poetry than it is to mathematical visual poetry. However, one could create a poem that has aspects of all three of these types. There are plenty examples of math type poems out there that use elements of visual mathematical poetry however, I have seen none that are done with the intent of having a didactic element within them and most if not all are too abstract to show the mechanics of visual mathematical poetry. Furthermore, I have not seen any that are ‘purely visual mathematical poetry to serve as clear example.
Verification of logic:
I have tested the logic in this piece on a group of aerospace engineers to see if the artistic aesthetic interfered with the logic. All of them clearly saw the logic and understood the mechanics of the piece however, a couple asked, in perfect stereotypical engineering demeanor, why would I bother.
I also presented this to the mathematician Paul Gailiunas who replied below:
"It goes further - there are special numbers if we do multiplication (the primes), but none in addition. Number theory follows. We can set up other systems that work like this, but the elements need not be numbers. They are called rings. Division is a further complication. Sometimes it works, and we have a "division ring", sometimes it doesn't. The integers do not form a division ring because things like 2/3 are not integers."
The mechanics of this piece:
What motivated this piece was some conversations with a few people who have trouble visualizing mathematical poetry in general and the difference between addition and multiplication in particular. I decided to create this piece to possibly help those people approach this nebulous concept. For if we look at addition we see 2 concepts put together in such away that the original concept is easy to remove from the other and both concepts are easy to identify retain their original identity. I think most people do not have much of a problem comprehending this idea. However, multiplication is much trickier to embrace. Using the operation of multiplication augments the result by integrating the identity of both elements being multiplied. That is in the example of 4 x 5 = 20. ‘Twenty’ can be seen to have been augmented by both 4 and 5 and one can see this by dividing up 20 by cutting out 5 pieces of 4 or 4 pieces of 5. What is important is that we recognize that 20 is a higher magnitude relative to both 4 and 5 but has the ‘identity’ of both 4 and 5. “Americana mathematics” operates the same way for in addition one can easily recognize and conceptually separate both identities. Furthermore, the multiplication operation has a result that is an augmentation of both separate identities but obviously is more powerful than the original ideas, has its own identity however; it retains the original identities of both.

For a web page version click here

Perelman and Me

Here is a timely mathematics poem by JoAnne Growny:



Perelman and Me

On Tuesday, August 22, 2006 Russian mathematician Grigory Perelman declined the Fields Medal for his contribution to the proof of a well-known and difficult conjecture first posed by Henri Poincare in 1904. I applaud Perelman’s seclusion.


The gravity of the universe
requires dark matter.
Choosing one thought
prevents another.

Little girls learn social graces
to make others feel at ease.
But friendly greetings
are never mathematics.

Difficult thoughts
are born in isolation :
genius slips away if socialized—
and so he must refuse the prize.

JoAnne Growney
25 August 2006

Why I Don’t Want To Teach (Math Joke#4)

Grumman on Schlegel

Bob Grumman has just posted Marko Niemi’s translation of Friedrich Schlegel’s equation for poetry and God on his blog at this URL: click here

Bob has made the following comments:

“This is a translation by Marko Niemi of the 19th-Century German philosopher Friedrich Schlegel’s formula for poetry. Kaz thinks it may be the world's first mathematical poem. I'm not sure. It seems mostly informrature to me--i.e., intended to inform rather than provide beauty, as literature is intended to do (in my poetics). It is a way of mathematically defining something philosophical as e equals mc squared mathematically defines energy, rather than creating a poetic experience. It is entirely asensual--at least for one like me, who has no notion what material feature "God" has. Mathematically, it is a little silly, too--for if "shit" were substituted for "FSM," the equation would be in no way altered. On the other hand, it is a marvelously step toward what Kaz and I and Geof and Karl are doing, perhaps a pivotal one (although I don't know of anyone who was inspired to create mathematical poetry by it).”

I would like to address a few things from his comments.

Bob says, “Kaz thinks it may be the world's first mathematical poem. I'm not sure.”

I would like to note that I doubt that this poem was the first mathematical poem ever written. It is however the earliest mathematical poem that I have seen. I have seen earlier mathematical visual poems but no mathematical poems this early. For an understanding of the difference between mathematical poem and mathematical visual poem, please check my terminology at this link: click here

Bob says, “It seems mostly informrature to me--i.e., intended to inform rather than provide beauty, as literature is intended to do (in my poetics).”

I see this as expressive rather than informative. The question to ask is, “Was Schlegel’s equation meant to be denotative or connotative. It is hard if not impossible to be denotative when you are dividing by zero. Concerning aesthetics, Bob has a very different idea of beauty than I and his views of mythology are very different from mine as well. Bob is certainly entitled to his opinion. Although I also would have to say that Schlegel’s view of God is about as different to my view as mine is to Bob’s. I think the main aesthetical point to Schlegel’s poem is tying “The Transcendent” to an expression of infinity … not just once but six times. There are many things beautiful to mathematicians and infinity is definitely one of them if not the greatest idea of beauty. On the other hand, those who believe in “God” would also believe that the idea of God is the greatest beauty. However, I am certain that my idea of God is heretical to those same believers, for I do not believe in using lower case letters for the ‘G’ in God. All Gods are metaphors to The Transcendent.

Bob says, It is a way of mathematically defining something philosophical as e equals mc squared mathematically defines energy, rather than creating a poetic experience.

Here Bob equates philosophy with science … That was certainly true in 300 BC. However, there is nothing scientific about this equation for a scientist in Schlegel's time would never divide by zero (it is undefined for scientific use but perfect for poetry in fact it is the crux of metaphor)
Here is Schlegel’s view:
“Schlegel argued that poetry should be at once philosophical and mythological, ironic and religious. As a literary critic Schlegel sought not to reveal objective truths, but to write criticism so that the usual discursive prose becomes a work of art itself.” **

Bob says, It is entirely asensual--at least for one like me, who has no notion what material feature "God" has.

I am confused … I do not know where ‘anything’ physical was stated or implied.

Bob says, Mathematically, it is a little silly, too--for if "shit" were substituted for "FSM," the equation would be in no way altered.

The latter statement is another aesthetic judgment and again Bob is entitled to any scatological view he desires ;)

Bob says, On the other hand, it is a marvelously step toward what Kaz and I and Geof and Karl are doing, perhaps a pivotal one (although I don't know of anyone who was inspired to create mathematical poetry by it).”

If Schlegel inspired anyone to write mathematical poetry then Marko Niemi may be the closest person to know for he is our source.


**The quote was taken from this web site: click here

Emerson Quote #2

Karl Kempton sent us this Emerson Quote:


Every word was once a poem.

-Ralph Waldo Emerson, writer and philosopher(1803-1882)

Emerson Quote #1:

Language is fossil poetry.

Ralph Waldo Emerson, writer and philosopher (1803-1882)

The Biggest Problem To Overcome With Math-Art

Waterfall by M. C. Escher 1961

The biggest problem to overcome with math-art in general is that it is tied to two mutually exclusive aesthetic ideas. One idea being that pure mathematics pervades all cultures. The second is that Art is the expression of a particular culture. Math being the language of logic shares the same logic in France as it does in China. Art may express an archetype but the ‘expression’ is cultural. I believe these two ideas are true in a broad sense although there is a little room for argument in the finer details.
I feel that using math as a language for art demands that the mathematical expression or structure has to have some relationship to the cultural idea put forward. There is much mathematical art expressed which is beautiful from a mathematical perspective but trivial from an art perspective. Furthermore, the converse of this is true as well. There is mathematical art that artists may find beautiful however, evokes yawns from the mathematics community.
I think the measure of success of any mathematical art lies in how well it is accepted by both communities. This is a very difficult task and there is a plethora of work accepted by one community but not the other. I think the most successful artist that is accepted by both communities is M C Escher. Even though his acceptance is expressed more by the math community than the art community this cannot be helped. Finding the middle ground would be near if not impossible. At the other end of the spectrum, I am going to risk saying that I believe you are delusional if you believe you have made great math art/poetry and you are accepted by only one community no matter how much croaking the one community does.

Why I Don’t Want To Teach (Math Joke#3)

Why I Don’t Want To Teach (Math Joke#2)

Hyper-Dimensional Poetry?

When I was first introduced to hyper-dimensional geometry I was quite fascinated but really didn’t have any clear path to understand it. I had seen two dimensional images of a hypercube (four-dimensional cube) but really understood nothing about what I was looking at. With computer imagery we are able to see things a little better because we can simulate three-dimensions in a video or other moving imagery. The following link will take you to a polytope slicer which allows you to take three-dimensional slices through a four-dimensional object.
Let me expound upon this a little bit. Just about all of us have experienced slicing a near two-dimensional piece of paper with a pair of scissors. When we do this we experience seeing a near one-dimensional line at the edge of the paper where we just cut. Many of us have also experienced slicing a ‘three-dimensional’ orange in half and noticing a two-dimensional surface showing the cells inside the orange. However things get a little trickier when we slice a four-dimensional object. If you notice on our previous examples that the slice is a dimension less than the object we started with. That is a slice of a three dimensional object is two-dimensional and a slice of a two-dimensional object is one dimensional. Therefore, to imagine a slice of a four-dimensional object our result would be something that has three-dimensions. Our polytope slicer does just that! It gives us a three dimensional-section cut of a four-dimensional regular polytope. Your next question may be, “what is a polytope?” A polytopes are to four dimensions as polyhedrons are to three dimensions or what polygons are to two dimensions.

As you vary the parameters in the polytope slicer you will get three-dimensional slices of our four-dimensional polytope. (click here for the polytope slicer).

Now what does this have to do with mathematical poetry? All maths can be used as language for poetry. Use your imagination … I predict that someone will write a poem on a hypercube so that we can read it by projecting it down to the third dimension. This may have already been done but I am not aware of it. After one does it with a hypercube then try doing it on a 120 cell hyperdodecahedron or maybe an epic poem on a 600 cell hypericosahedron

Why I Don't Want To Teach (Math Joke#1)

Here is a math joke sent to me by Aerospace engineers Paul Mossel and Keith Rowley on the subject of why I don’t want to teach.