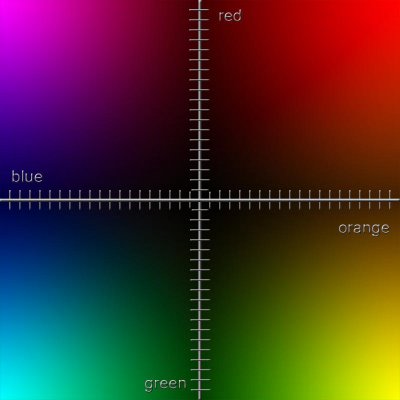
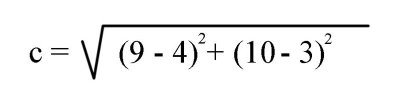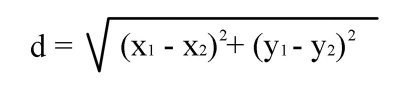2.2. Word-coordinate Pairs: We have witnessed a word-axis with different values of an antonym pair along a particular axis 'x' or 'y' in one dimension. (See figure 3) We also have seen a word-plane with values of two antonym pairs along two axes 'x' and 'y' in two dimensions. (See figure 10) Furthermore, we can have word-cubes along the x, y, and z-axes in the third and word-hypercubes in the fourth dimension or we can have antonymic pairs in innumerable dimensions. There is no limit to the dimensional palette for our expressions. Each antonym word-pair adds a new spatial dimension to our expressive construction. Let us talk about the spatial accuracy in defining the location of words in space. Once again, let us look at figure 10 and notice the antonym word pairs, just/unjust and noble/ignoble. However, let us focus our attention to the word-axis just/unjust. We know that we have defined a one-dimensional word-axis with different values of just and unjust but we do not know exactly where each of the words is located along the axis. We have no quantitative value for just or unjust. However, we do have a qualitative value and we know that the word exists somewhere on the axis. What is most important to us in verbogeometry is not the value as such, but the spatial relationship of the values to each other in space. Because the value or the meaning of a word is relative to the context in which it is used, each viewer individually creates his or her own context for meaning. Therefore, exact quantification of the word or its location in space is not possible. However, in some cases, it may be possible to restrict the context to a level where repeatable correlations exist, but those studies are more akin to denotation for the purpose of science. Scientific experimentation "proves" the equation to be mathematically correct and workable within a range of acceptability. In other words, experimental data defines viability of the relationships between the concepts in a scientific equation. On a side note: (When scientific equations are in the intuitive stages of development, there may be an argument to claim that they are in the realm of art, I personally might accept this view if it were not for the fact that their intention is not to make art.) In verbogeometry, we construct equations based on relationships between the qualities of our experiences to evoke meaningful aesthetic expressions of which most are connotative but some may be denotative.Let us get back to the Cartesian coordinate system for a moment and reiterate the idea of coordinate pairs. A point on a two dimensional coordinate system would have values for x and y and would be expressed as such: (x,y) (see figure 1.) A point on a three-dimensional axis system would have values for x, y and z and would be expressed as (x,y,z). A four dimensional point would be expressed as (x,y,z,w) in the fifth dimension as (x,y,z,w,v) etc.Before we get into multidimensional word-axes let just look at a simple two-dimensional word-plane with two word-axes. (see figure 12.)
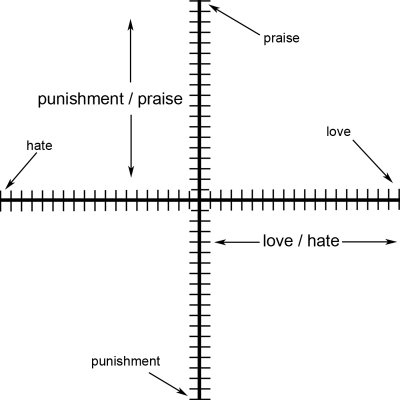
Figure 12
The vertical axis is a synonym word-pair of praise and punishment and the horizontal axis is a synonym word-pair of love and hate. It is very important to realize that not only does the words love and hate define the identity of the horizontal or x-axis they also hold conceptual points in space along the axis and the same for praise and punishment with respect to the y-axis. The words which are conceptual points in space define a metaphoric value along its respective axis and can be notated as a coordinate pair similar to (x,y) So you may ask what would a coordinate word-pair look like? Let us look at the two points identified as point 1 or P1(love,praise) and point 2 P2(hate,punishment) (see figure 13.)

Figure. 13